电子衍射及其花样形成原理

电子衍射是周期性排列的晶体结构对电子发生弹性散射的结果。当电子与晶体物质作用时,电子受到原子集合体的散射,在弹性散射的情况下,各电子散射的电子波波长相同,由于晶体中原子的周期性排列,使得散射电子波满足相干条件,在相遇区域相干叠加,从而形成相干散射,在某些方向干涉加强出现电子衍射现象。电子受到试样的弹性散射是电子衍射图和电子显微镜的物理依据,它可以提供试样晶体结构及原子排列的信息。

电子衍射分为低能电子衍射(加速电压仅有10～500 V)和高能电子衍射(加速电压一般在100 kV以上),透射电镜采用的是高能电子衍射,主要用于材料的物相和结构分析、晶体位向的确定和晶体缺陷及其晶体学特征的表征等方面。

1)电子衍射方向

电子衍射束在空间方位上如何分布?布拉格方程从数学的角度给出了解答,而厄瓦尔德图解以作图的方式回答了这个问题,二者是等效的。

(1)布拉格(Bragg)方程

由于晶体结构的周期性,可将晶体视为许多相互平行且晶面间距相等的原子面组成,即认为晶体是由晶面指数为(hkl)的晶面堆垛而成,晶面间距为d,设一束平行的入射波(波长λ)以θ角照射到(hkl)的原子面上,各原子面产生反射。

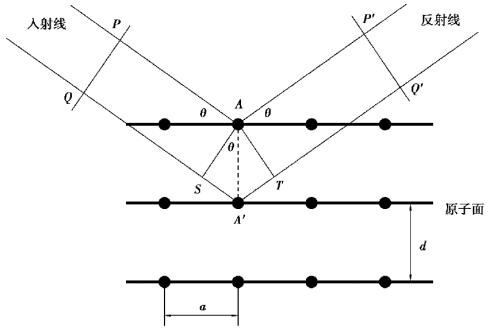
图5.3　布拉格反射原理图

图5.3中PA和QA′分别为照射到相邻两个平行原子面的入射线,它们的反射线分别为AP′和A′Q′,则两条反射线的光程差为

只有当光程差为波长的整数倍时,相邻晶面的反射波才能干涉加强形成衍射线,所以产生衍射的条件为

式(5.5)是著名的布拉格公式,其中n=0,1,2,3,…称为衍射级数,θ角称为布拉格角或半衍射角。

布拉格方程包含很多对材料分析非常重要的含义:

①衍射是一种选择性反射,只有当λ、θ、d三者之间满足布拉格方程时才能发生反射,进而产生衍射现象。

②入射线的波长决定了结构分析的能量,只有晶面间距大于的晶面才能产生衍射,衍射分析用入射线波长应与晶体的晶格常数接近。

③衍射花样和晶体结构具有确定的关系,将各晶系的晶面间距方程代入布拉格方程(n=1,且只适用于简单晶胞)

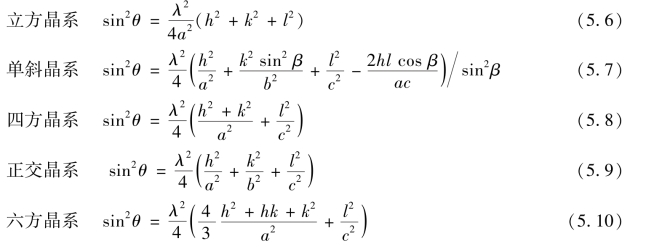
会发现不同晶系的晶体、同一晶系而晶胞大小不同的晶体的各种晶面对应衍射线的方向θ不同,因此对应的衍射花样是不同的。即衍射花样可以反映出晶体结构中晶胞大小及形状的变化。

(2)厄瓦尔德(Eward)图解

厄瓦尔德于1921年建立了倒易点阵的方法,倒易点阵是一种由阵点规则排列构成的虚拟点阵,它的每一个点阵和正空间相应的晶面族有倒易关系,即倒空间的一个点代表着正空间的一族晶面。倒格矢(倒易矢量)Ghkl=hb1+kb2+lb3,其中(hkl)为正空间点阵中的晶面指数,Ghkl垂直于正空间点阵中的晶面(hkl),而且倒格矢的长度等于正点阵晶面(hkl)间距的倒数|Ghkl|=1/dhkl。(www.zuozong.com)

厄瓦尔德(Eward)图解法是将布拉格方程用几何图形直观地表达出来,即Eward图解法是布拉格方程的几何表达。

①厄瓦尔德(Eward)球。

厄瓦尔德(Eward)图解法是在倒易空间中,画出衍射晶体的倒易点阵,以其中任一格点为倒易原点O,以O为端点作入射波的波矢量S0(即图5.4中的矢量O1O),该矢量平行于入射方向,长度等于波长的倒数1/λ。以O1为中心,1/λ为半径作一个球,这就是Eward球(也称为反射球)。此时,若有倒易阵点Ghkl正好落在Eward球的球面上,则相应的晶面(hkl)与入射方向必然满足布拉格方程,而衍射波方向就是O1G(对应波矢量为S),其长度也等于波长的倒数1/λ。

②厄瓦尔德(Eward)图解。

由于AO为Eward球的直径,所以△AOG为直角三角形,因此有

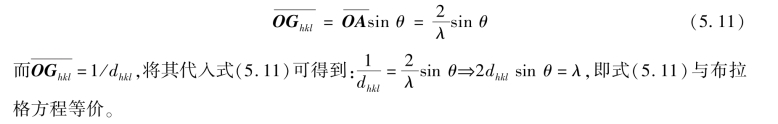
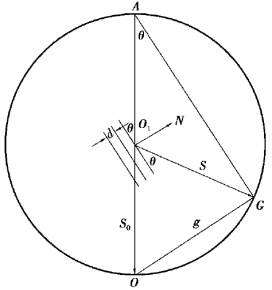
图5.4　厄瓦尔德图解

由图5.4可见,倒易矢量g=S-S0(OG=O1GO1O),即当衍射波矢和入射波矢相差一个倒格子时,衍射才能产生。这时倒易格点刚好落在Eward球的球面上,产生的衍射方向沿着球心到倒易格点的方向,相应的晶面(hkl)与入射波束满足布拉格方程。

2)电子衍射的强度

影响衍射强度的因素较多,一般从散射基元(单电子)对入射波的散射强度开始处理,首先计算一个电子对入射波的散射强度(涉及偏振因子);再将原子内所有电子的散射波合成,得到一个原子对入射波的散射强度(涉及原子散射因子);其次将一个晶胞内所有原子的散射波合成,得到晶胞的衍射强度(涉及结构因子);而后将一个晶粒内所有晶胞的散射波合成,得到晶粒的衍射强度(涉及干涉函数);最后将材料内所有晶粒的散射波合成,得到材料(多晶体)的衍射强度。另外在实际测试条件下材料的衍射强度还受温度、材料吸收以及等同晶面数等因素的影响,因此在衍射强度公式中还须引入温度因子、吸收因子和多重性因子。

3)电子衍射花样的形成原理

电子衍射花样是电子衍射斑点在正空间中的投影,图5.5为电子衍射花样的形成原理图。试样位于Eward球的球心O1处,电子束从AO1方向入射,作用于晶体的晶面(hkl)上,若该晶面刚好满足布拉格条件,则电子束将沿着O1G方向发生衍射并与反射球相交于G。在试样下方L处放置一张底片,就可让入射波束和衍射波束同时在底片上感光成像,结果在底片上形成两个像点O2和G1,如图5.5(a)所示。当晶体中由多个晶面同时满足衍射条件时,球面上有多个倒易点阵,在底片上分别成像,从而形成以O2为中心,多个像点分布四周的衍射花样谱,如图5.5(b)所示。此时,O点和G点是倒易空间的阵点,是虚拟存在点,而底片上的像点O2点和G1点则已经是正空间中的真实点了,这样Eward球上的倒易阵点通过投影转换到了正空间。

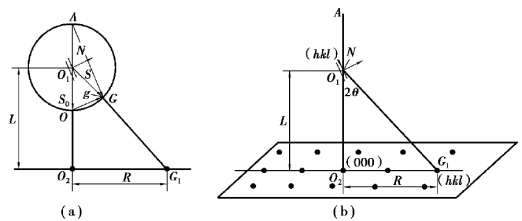
图5.5　衍射花样的形成原理

设底片上的像点G1和中心点O2的距离为R,衍射角很小,可以近似认为g⊥S,因此△O1OG与△O1O2G1相似,有

令R为透射斑点O2到衍射斑点G1的连接矢量,令K=λL,则有

式(5.13)为电子衍射的基本公式,K=λL称为相机常数;L为相机长度。这样正、倒空间就通过相机常数联系在一起了,晶体中的微观结构可通过测定电子衍射花样,经过相机常数K的转换,获得倒空间的相应参数,再由倒易点阵的定义就可推测各衍射晶面之间的相对位向关系了。