结构设计原理-3.5.4计算内容和T形截面的弯矩

1.截面选择

T形截面尺寸一般是预先假定或参考雷同的结构或根据经验数据取用（梁的高宽比h/b＝2～8，高跨比h/l＝1/16～1/11）。

截面尺寸确定之后，首先应用判别式［式（3-46）或式（3-48）］确定构件截面属于何种T形截面。

（1）第一种T形截面。设计方法与宽、高分别为b_f′、h的单筋矩形截面完全相同。

（2）第二种T形截面。已知设计值M_d，截面尺寸b、h、b_f′、h_f′，混凝土强度等级和钢筋牌号，结构重要性系数γ₀，计算受拉钢筋截面面积A_s。

计算步骤：

1）求翼缘部分混凝土所承受之压力对受拉钢筋合力作用点的力矩：

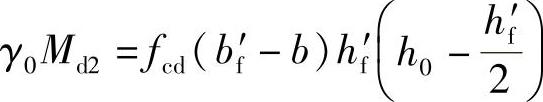
2）如图3-23c所示，根据翼缘挑出部分的受压区内力f_cd（b_f′-b）h_f′与一部分受拉钢筋A_s2的内力f_sdA_s2的平衡条件，计算这部分受拉钢筋截面面积A_s2，即：

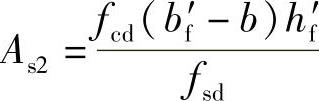
3）取γ₀M_d＝γ₀M_d1+γ₀M_d2，得M_d1＝M_d-M_d2，再按单筋矩形截面的计算方法，求出平衡中性轴以上腹板部分混凝土压力所需的受拉钢筋截面面积A_s1，即由式（3-20）先求出受压区高度x，再由式（3-21）求得A_s1：

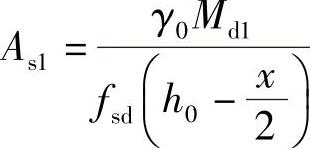
4）求受拉钢筋总截面面积：

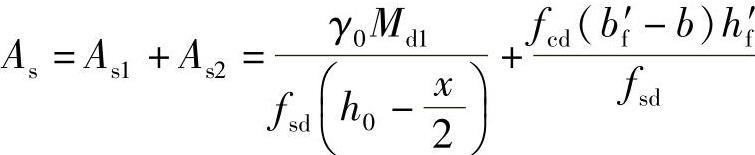
5）计算中性轴位置：

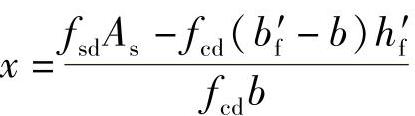
核算是否满足x≤ξ_bh₀的适用条件。

【例3-6】 某钢筋混凝土T形梁，已定截面尺寸如图3-25所示，跨中截面弯矩组合设计值M_d＝735kN·m，结构重要性系数γ₀＝1.1，拟采用C25混凝土（f_cd＝11.5MPa）、HRB335钢筋（f_sd＝280MPa），求受拉钢筋截面面积A_s。

解：首先判别T形截面的类型。设此T形截面受拉钢筋为两排，取a_s＝80mm，则有h₀＝h-a_s＝（1000-80）mm＝920mm。

因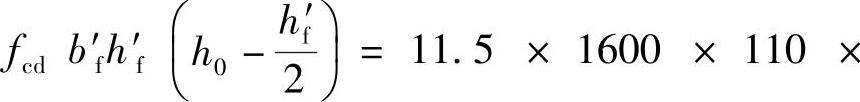

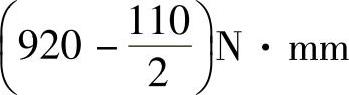
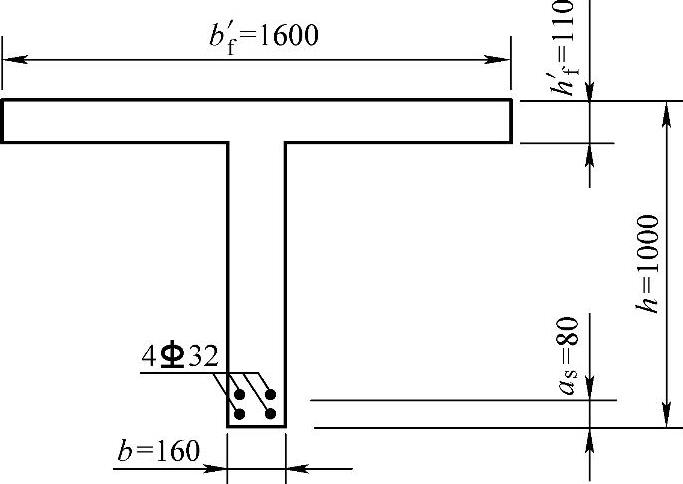
图3-25 T梁截面

＝1750.76kN·m＞γ₀M_d＝1.1×735kN·m＝808.5kN·m

由式（3-46）可判定此截面属于第一种T形截面，可按矩形截面b_f′×h进行计算。

由式（3-20）求出受压区高度x：

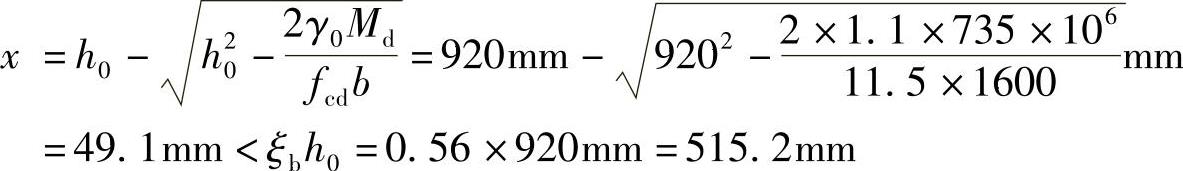
由式（3-22）求出受拉钢筋截面面积A_s：

现取用432，则实际取用的受拉钢筋截面面积A_s＝3217mm²。钢筋布置如图3-25所示。

实际取用受拉钢筋重心至下边缘的距离：

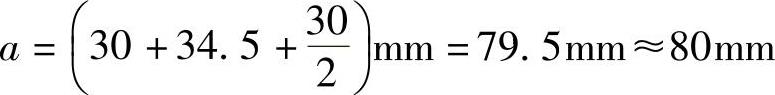
实际配筋所需腹板宽：

b＝（30+34.5+30+34.5+30）mm＝159mm＜b＝160mm，符合要求。

2.承载力复核

对已设计的T形截面梁进行正截面承载力复核时，首先应用式（3-45）或式（3-47）判别构件截面属于何种T形截面，然后再按有关公式进行承载力的复核。

（1）第一种T形截面：承载力复核内容与单筋矩形截面b_f′×h相同。(www.zuozong.com)

（2）第二种T形截面：承载力复核可按下列步骤进行：

已知弯矩组合设计值M_d，截面尺寸b、h、b_f′、h_f′，混凝土强度等级和钢筋牌号，结构重要性系数γ₀，受拉钢筋截面面积A_s及其布置情况，验算截面所能承担的弯矩M_u，并判断其安全程度。

计算步骤：

1）由图3-23c求平衡翼缘挑出部分混凝土压力所需受拉钢筋截面面积A_s2：

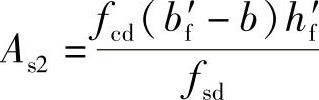
2）计算平衡梁腹部分混凝土压力所需受拉钢筋截面面积A_s1＝A_s-A_s2。

3）由配筋率从计算。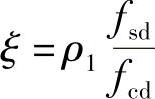

4）计算，。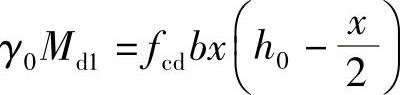

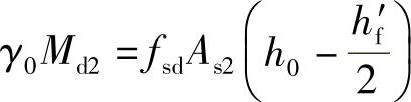5）计算该截面实际所能承担的弯矩：M_u＝γ₀M_d1+γ₀M_d2。

比较M_d与M_u，判断其安全程度。若M_d≤M_u，承载力满足要求；若M_d＞M_u，承载力不满足要求。

【例3-7】 某整体式∏形梁格系中一小纵梁，计算跨径l＝6m，截面如图3-26所示，结构重要性系数γ₀＝1.1，弯矩组合设计值M_d＝330kN·m，梁截面尺寸b＝200mm，h＝500mm，与两侧主梁间距为2.40m，净距为2.20m，翼缘h′_f＝80mm，拟采用C20混凝土（f_cd＝9.2MPa），HRB400钢筋（f_sd＝330MPa），纵向受拉钢筋采用6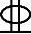25，其截面面积A_s＝2945mm²，钢筋截面重心位置a_s＝71mm，求该小纵梁截面的承载力，并判断其安全程度。

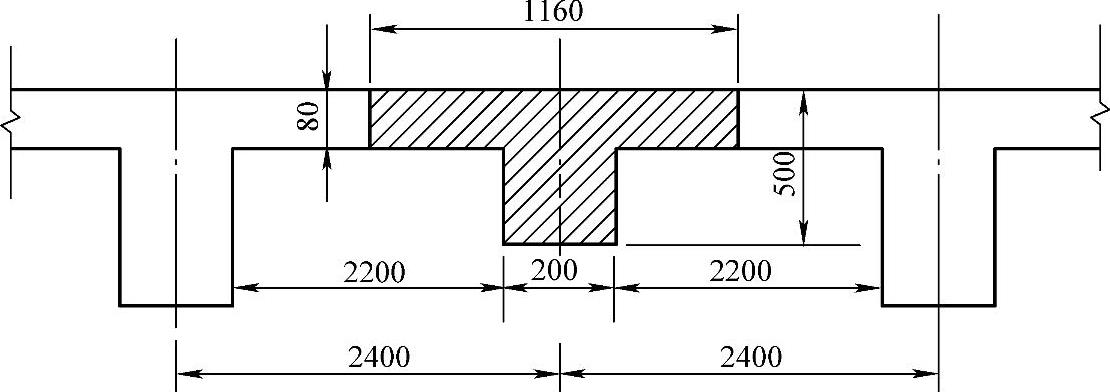
图3-26 ∏形梁截面

解：确定此副纵梁翼缘计算宽度b_f′：

1）计算跨径的1/3——l/3＝6000mm/3＝2000mm。

2）相邻两片梁轴线间距离2400mm。

3）b+2c+12h_f′＝（200+0+12×80）mm＝1160mm。

取上述三者的最小值，即计算宽度b_f′＝1160mm。

判别截面的类型：

截面有效高度h₀＝h-a_s＝（500-71）mm＝429mm

由f_sdA_s＝330×2945N＝971.85kN，f_cdb_f′h_f′＝9.2×1160×80N＝853.76kN，可得f_sdA_s＞f_cdb_f′h_f′，该截面属第二种T形截面。

求平衡翼缘挑出部分混凝土压力所需受拉钢筋截面面积A_s2：

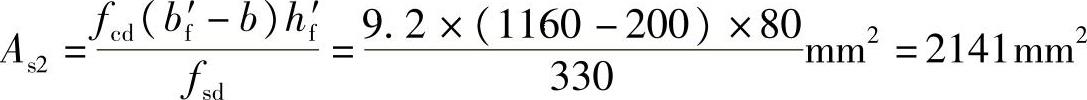
则平衡中性轴以上腹板部分混凝土压力所需受拉钢筋截面面积A_s1：

A_s1＝A_s-A_s2＝（2945-2141）mm²＝804mm2

其对应配筋率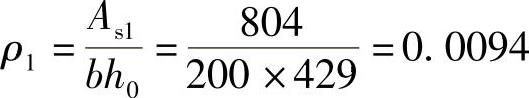

对应的受压区高度系数：

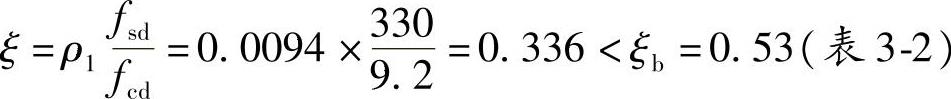
由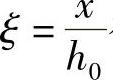

得：x＝ξh₀＝0.336×429mm＝144.14mm

再由式（3-8）得：

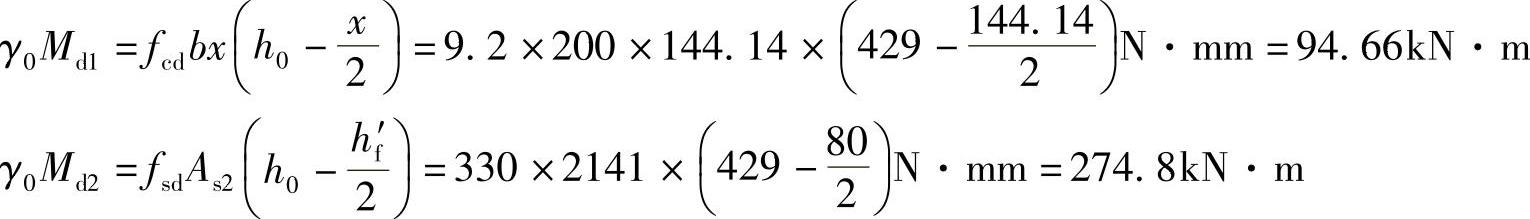
所以此小纵梁截面的承载力为

M_u＝γ₀M_d1+γ₀M_d2＝（94.66+274.8）kN·m＝369.46kN·m＞γ₀M_d＝1.1×330kN·m＝363kN·m

满足承载力要求。