脉冲响应分析：理论与应用

在进行脉冲响应分析之前，先要对模型进行稳定性检验，即看单位根的倒数是否都落在单位圆之内，如果都落在单位圆之内，则表明模型是平稳的，可以进行脉冲响应分析和方差分解。结果如下所示，结果表明构建的VAR模型是稳定的，可以进行脉冲响应分析。

由于VAR模型并非是一个理论性的模型，对于变量无需做任何先验性约束，因此在实际分析时，往往不研究一个变量对两一个变量的影响如何，而是分析当一个误差项发生变化时，或者说模型收到某种冲击时对系统的动态影响，即脉冲响应函数的方法。脉冲相应函数是用于衡量随机扰动项的一个标准差冲击对内生变量当前和未来取值的影响。在已建立的VAR模型基础上，分别对FBC和FPC做外生冲击，来观察这种冲击对另外一个变量的当前值和未来值的影响。本书构建的VAR模型为VAR2、，具体形式为：

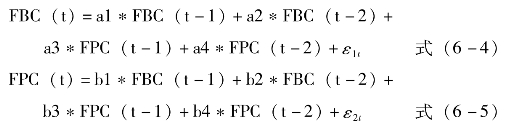
假定随机扰动项是具有如下性质的白噪声向量：

E（εit）=0，对于∀t，其中i=1，2

var（εt）={σij}，对于∀t

E（εitεis）=0，对于∀t≠s，i=1，2

另假定上述系统从0期开始活动，且FBC（t-1）=FBC（t-2）=FBC（t-1）=FBC（t-2）=0，另设第0期给定了扰动项ε10=1，ε20=0，并且其后均为0，即ε1t=ε2t=0（t=1，2，……）称此为第0期给FBC以脉冲，此时FBC（0）=1，FPC（0）=0，将其结果带入式（6-4）和（6-5）中，得到t=1时，FBC（1）=-0.043730，FPC（1）=0.073276。依次迭代运算下去，即得到由FBC脉冲引起的FBC的响应函数，同样方法可以得到由FBC脉冲引起的FPC的响应函数。如果第0期的脉冲反过来，从ε10=0，ε20=1出发，即得到由FPC的脉冲引起的FPC和FBC的响应函数。响应函数能够明显地捕捉到外生冲击对于经济变量的冲击效果，在本章中能够用来分析宏观经济运行冲击和价格冲击能够引起双方的变化的方向与大小。(www.zuozong.com)

1.FBC脉冲引起FPC的响应

FBC对FPC的脉冲响应结果如图6.3所示。当在本期给FBC一个标准差单位的冲击后（冲击类型为暂时冲击，可以假设为某种消费冲击、需求冲击或者供给冲击），FPC产生正向波动，这种正增长会随着时间的推移逐渐减小，到第4期时回归到0，之后开始向下运动，产生负向变化，到第8期时回复到原始位置。这表明对FBC的一个新息标准差冲击会在前4期会使FPC有同向变化，这种变化随时间推移逐渐减小，在第4至第8期冲击影响转为负向。FPC的变化不具有持续性，最终会回到原位置。

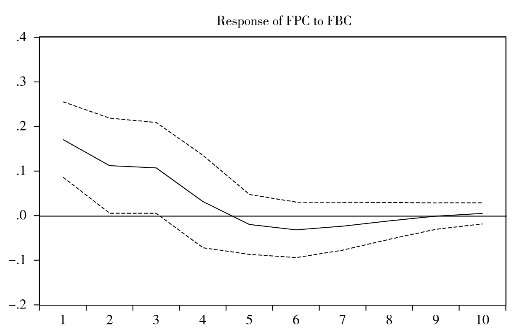
图6.3　对FPC冲击引起FBC的响应图

2.FPC脉冲引起FBC的响应

FBC对FPC的脉冲响应结果如图6.4所示。当在本期给FPC一个新息标准差单位的外生冲击后（冲击类型为暂时冲击，假设为某种价格冲击），FBC在半期之后开始有正向的增长反应，这种正向反应在第2期时达到最大值，之后随着时间的推移逐渐减弱，到第2期末回归至零值，之后继续下行，持续一段时间负值后，第5期时再次回到零值，之后持续一段时间弱正向反应回归到零。这表明对FPC的一个外生的暂时性冲击会使FBC在前两期有同向的反应，在第3至第4期这种冲击的影响会转化为负向，但不具有持续性，最终会回复到原始位置，持续一定的弱正向变化后影响消失。

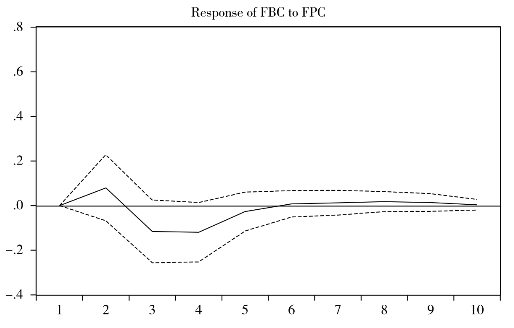
图6.4　对FBC冲击引起FPC的响应图