光伏电站数据异常识别与修复技术优化方案

2.1.1.1　光伏电站异常数据识别方法

（1）光伏电站输出功率数据主要异常类型

在风功率数据预处理时，数据的异常值检查主要有：数据有效性检查；缺失数据检查；风机信号延迟检查等步骤。借鉴风功率异常数据处理方式，并结合实际光伏电站输出功率的特点，将光伏电站输出功率数据的主要异常类型分为如下三类。

1）数据丢失，表现为数据空缺，主要由通信中断引起，如图2-1所示：

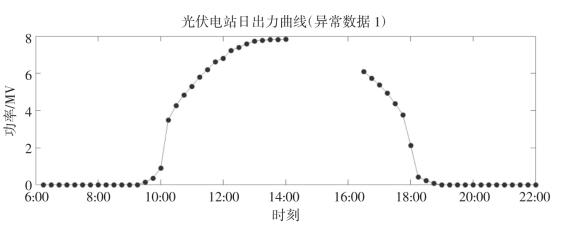
图2-1　第一类异常数据

2）数据超出正常范围（如图2-2所示），主要由通信误码、监测异常、数据存储异常等原因引起。

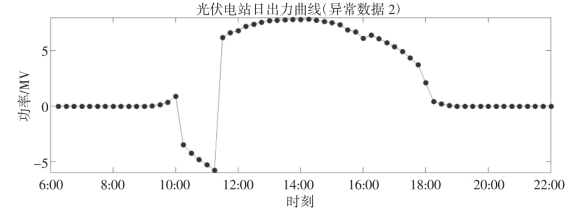
图2-2　第二类异常数据

3）数据与实际值偏差较大（如图2-3所示），除了第一类和第二类异常数据外，由于监测异常等原因导致记录数据在正常范围内，但与实际值偏差较大。

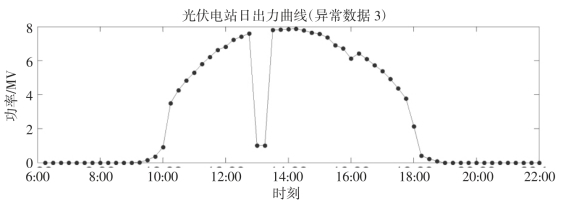
图2-3　第三类异常数据

（2）光伏电站数据异常判据

1）第一类异常数据识别

通过数据样本识别是否存在空缺值，具体如下：

设X={x1，x2…xi}为光伏电站时序输出功率，若存在xi满足：

则判断xi存在数据丢失。

2）第二类异常数据识别

通过数据识别是否超出正常数值范围上下限，具体如下：

若存在xi满足下式关系，则判断xi超出正常数值范围：

式中，xh和xi分别为正常数值范围上限和下限。

3）第三类异常数据识别

相邻电站的功率通常具有相似趋势，故利用相邻电站的功率数据对观测电站的功率数据进行校验，识别异常数据，具体如下：

设XA={xA1，xA2…xAi}为相邻电站A的时序输出功率，归一化后得到

设两个电站归一化后的功率差值为ei

不同电站、不同时间段获得的功率数据异常情况不同，为得到较高可信度的识别结果，对于已剔除第一类和第二类异常数据的待识别数据集，计算与相邻电站输出功率差的平均值和标准差。然后根据莱以特准则判断异常数据，即ei与功率差平均值的偏差大于标准差3倍时，认为xi为第三类异常数据。

（3）光伏电站异常数据识别流程

针对前述三类异常数据的特点，本文对异常数据进行识别和筛选，主要步骤如下。

第一步：数据输入；

第二步：提取光伏电站功率数据特征，确定不同类型异常数据判别的阈值；

第三步：筛选电站数据中的空缺数据；

第四步：在非空缺数据中，筛选出超出正常范围数据；

第五步：在剩余数据中筛选出与实际值偏差较大数据。

2.1.1.2　光伏电站数据修复方法

（1）基本思路

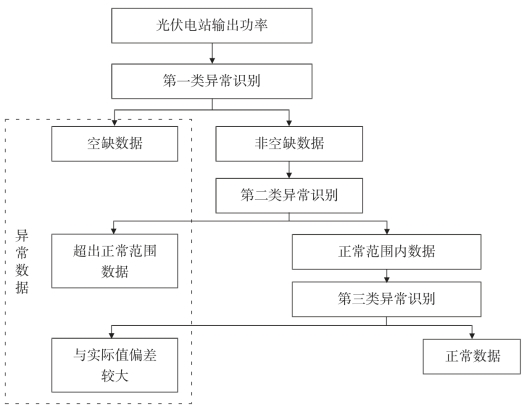
图2-4　光伏电站异常数据识别流程

若不考虑设备运行状态差异对光伏电站输出功率的影响，对于相似的天气、气温等气象条件，光伏电站输出功率也会呈现相似性，故可以选择历史数据中具有“相似日”或“相似天气模式”的输出功率对光伏电站功率数据进行修复。此时，光伏电站输出功率数据修复的可信度在很大程度上依赖于历史数据的准确性。

考虑到同一区域内的光伏电站通常具有基本相同的气象条件，其输出功率存在较强的相关性，若能够借助相邻电站的数据辅助功率数据修复或对修复数据进行校验，将会大大提高修复数据的可信度。

提出一种考虑天气和空间相关性的光伏电站输出功率数据修复方法，在原有只考虑天气的“相似日”的数据修复方法基础上，增加“相关电站”辅助修复和校验。该方法扩充了光伏电站数据修复的应用场景，同时有助于提升光伏电站异常数据识别及修复的可信度：

1）在仅存在“相似日”的情况下，可采用已有方法进行数据修复；

2）若不存在“相似日”，可借助“相关电站”解决数据修复问题；

3）若“相似日”和“相关电站”同时存在，可借助“相关电站”的数据对原方法的修复数据进行验证。

（2）相关系数

对于两个随机变量{（xi，yi）}之间的关系，通常采用相关系数进行描述。皮尔逊积矩相关系数（Pearson's product correlation coefficient，PPMCC），肯德尔秩次相关系数（Kendall's tau，KT）和斯皮尔曼秩次相关系数（Spearman's rho，SR）最为经典，应用最为广泛。本文的分析采用皮尔逊积矩相关系数rp，其定义为：

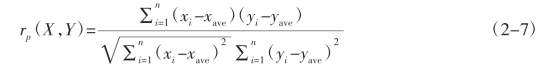
式中，xave和yave分别代表X和Y的算术平均。

相关系数取值在-1到1之间，r=0时，称X，Y不相关；r=1时，称X，Y完全相关，此时，X，Y之间具有线性函数关系；r<1时，X的变动引起Y的部分变动，r的绝对值越大，X的变动引起Y的变动就越大，r>0.8时称为高度相关，当r<0.3时称为低度相关，其他时候为中度相关。

（3）训练样本的选取

1）“相似日”的选择

“相似日”是依据历史天气信息的相关程度来判断的。设Wi={w1，w2，w3，w4}为描述光伏电站天气模式的数据集，包含了天气类型（如表2-1所示）、最高气温、最低气温和平均气温信息。

表2-1　广义天气对应表

依据式（2-7），在计算第k日与第i日天气相关系数，形成Wk与Wi（i=1，k-1，k+1，…，n）的相关系数集{rwki}，确定阈值α（根据实际情况设定），按式（2-8）选择满足相关性要求的“相似日”：

2）“相似电站”的选择

设待修复光伏电站为电站A，在m日内的时序输出功率为XB={xB1，xB2，…，xBm}，若同区域内还有相邻光伏电站B、C、D、E，其时序输出功率分别为XC={xC1，xC2，…，xCm}，XD={xD1，xD2，…，xDm}和XE={xE1，xE2，…，xEm}。分别计算光伏电站A与电站B、C、D、E的功率相关系数rAB，rAC，rAD，rAE，确定阈值β（根据实际情况设定），选择满足式（2-9）的电站，将该电站确定为“相似电站”，并将相应数据作为训练样本。

(www.zuozong.com)

α和β这两个相关系数阈值选取基本原则是考虑高度相关情况，即阈值大于等于0.8，取过高可能会导致相似日或相关电站样本太少，对神经网络模型训练造成困难，相关系数阈值选取过低可能会导致修复精度下降。因此，有必要根据样本数据及数据修复的精确度要求合理选择阈值。

3）训练样本

根据历史数据特点，用于光伏电站发电功率数据修复的训练样本可能出现下列3种情况：

①仅存在“相似日”时，训练样本为待修复电站在“相似日”的历史数据；

②仅存在“相似电站”时，训练样本为“相似电站”的历史数据；

③“相似日”和“相关电站”同时存在时，训练样本为“相关电站”在“相似日”的历史数据。

其中，情况1的修复数据可信度取决于电站自身历史数据的可信度，情况2的修复数据可信度取决于“相关电站”输出功率数据的可信度，情况3的修复数据可信度最高。

（4）数据修复方法和流程

考虑到光伏电站输出功率的复杂非线性，本文采用BP神经网络算法实现数据修复（如图2-5所示）。将训练样本输入BP神经网络模型进行模型训练，并将输出得到的数据作为第i日待修复电站功率修复值。考虑到训练样本可能出现的三种情况，BP神经网络实现数据修复的输入变量会有所区别，具体如表2-2所示。

表2-2　BP神经网络模型输入输出变量

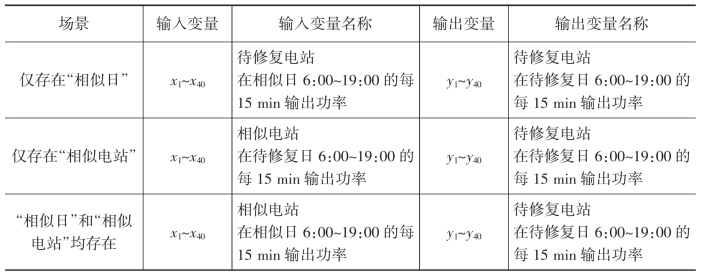
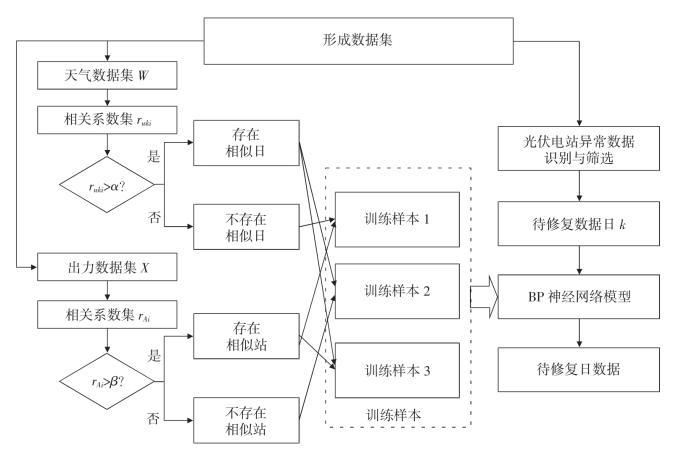
图2-5　光伏电站输出功率修复方法流程图

2.1.1.3　光伏电站“场-网”数据一致性实例分析

以光伏发电为例，选取青海格尔木地区四座光伏电站功率实测数据进行分析。四座电站为BK、HH、BC和SG，装机容量分别为10 MW、250 MW、20 MW和25 MW。以BK电站为对象验证本文方法。数据记录时间区间为2015年1月6日至10日，采样间隔为15 min。为对比修复结果的可信性，构造常见异常数据，将修复结果与原始值进行对比。

（1）相关性分析

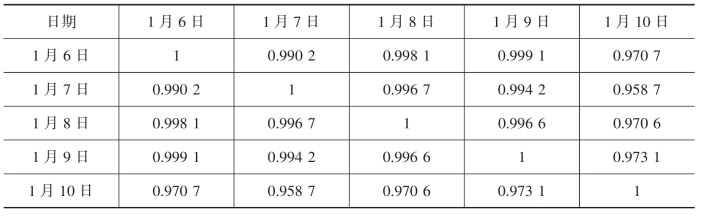
以2015年格尔木地区光伏数据为例，2015年1月6日至10日格尔木地区天气情况（如表2-3所示），通过相关系数的计算（如表2-4所示），可以看出这五天的天气具有强相关性。

表2-3　格尔木地区天气情况

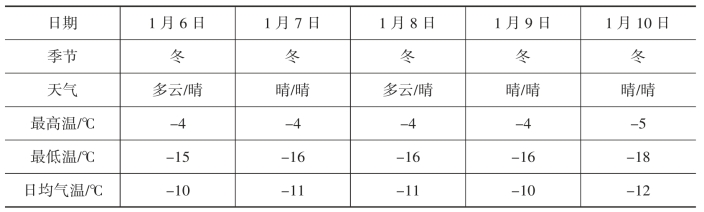
表2-4　天气相关系数表

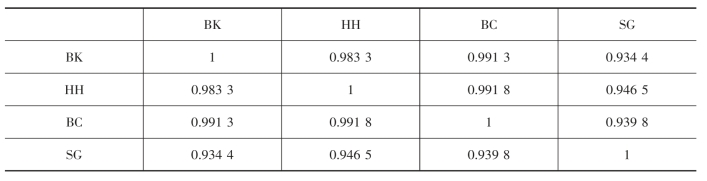
四座光伏电站2015年1月6日至1月10日的功率曲线如图2-6所示，曲线的峰值因电站的装机容量而不同，但趋势一致。四座光伏电站输出功率的相关系数如表2-5所示，BK电站与HH电站、BC电站及SG电站的日输出功率相关性都较高，其中与BC电站的输出功率相关性最高。

图2-6　四座光伏电站功率曲线

表2-5　电站功率相关系数表

（2）构造异常数据场景

为能够对比数据修复效果，构造BK电站2015年1月8日输出功率数据异常和缺失场景：

1）删除10：00～11：00数据；

2）将11：00～12：00的数据修改为原始数据的0.6倍；

3）将15：00～16：00的数据修改为大于装机容量的异常值。构造异常场景后的日功率输出曲线如图2-7所示。

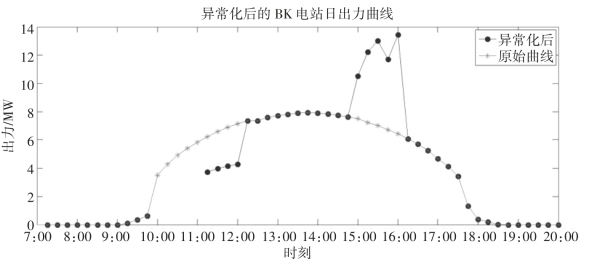
图2-7　BK电站日功率输出（异常）曲线

（3）异常数据识别

采用上文中的方法，识别异常数据。

1）10：00～11　：00时段

该时段对应输出功率集合X10-11={x41，x42，x43，x44，x45}，X10-11=Ø属于第一类异常数据类型。

2）11：00～12　：00时段

该时段对应输出功率集合X11-12={x46，x47，x48，x49}，与BC电站相同时间的归一化输出功率差值如表2-6所示。

表2-6　BK电站与BC电站归一化输出功率差值

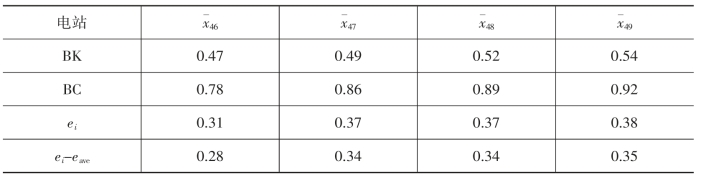
计算1月6日至1月10日时间段内，各个时刻的BK电站与BC电站归一化输出功率差值ei，进而得到均值和标准差分别为0.03和0.045。x46，x47，x48，x49的功率差值满足莱以特准则，故均为第三类异常数据。

3）15：00～16　：00时段

该时段对应输出功率集合X15-16={x61，x62，x63，x64，x65}，x61=10.50，x62=12.21，x63=13.01，x64=11.71，x65=13.42，属于第二类异常数据类型。

（4）异常数据修复

1）与传统方法结果比较

由上文中相关性分析得到，设相关系数阈值α=β=0.8，则“相似日”为1月6、7、9、10日，“相关电站”为HH、BC、SG电站，采用相关电站在相似日的输出功率数据作为输入，训练神经网络模型。得到修复后的BK电站1月8日输出功率曲线与原始曲线如图2-8所示。

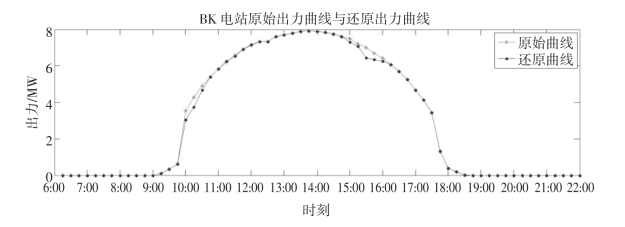
图2-8　BK电站原始功率曲线与修复的功率曲线

由图2-8可见，数据修复精确性良好，修复后的电阻输出功率与原始输出功率偏差很小。表2-7为BK电站原始功率数据、采用本文方法修复后的功率数据及传统插值法修复后的功率数据。

表2-7　原始值及修复值对比表

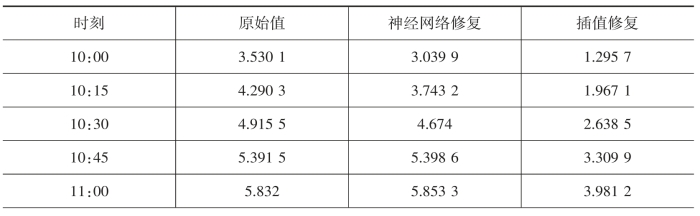
续表

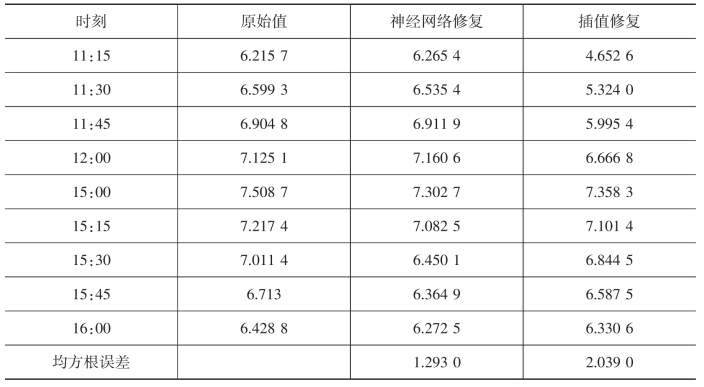
由表2-7可知，相比传统插值方法，考虑电站功率相关性修复得到的功率数据与原始值更为接近，考虑电站输出功率相关性的神经网络修复方法具有良好的还原精度。

（5）BK光伏电站全年功率数据修复结果

采用上述方法，对BK光伏电站全年实测数据（采样间隔15 min，全年共计35 040个点）进行异常数据识别和修复，绘制修复前后输出功率等高线图，如图2-9和图2-10所示。功率等高线图中，横轴是以日为精度的时间轴，变化范围是2015年1月1日至2015年12月31日；纵轴是以15 min为精度的时间轴，变化范围是从0：00时刻至23：45时刻；不同颜色的点对应不同的功率值，因此功率等高线图清晰地描绘了一年中每个采用点的功率大小。在原始数据中，如图2-9所示，图中存在较多明显的功率异常情况，如数据缺失（空白点）和夜间持续稳定出力情况（纯色柱状线条）等。采用本文所述方法得到的结果如图2-10所示，可以看到，本文所采用的方法对异常数据识别效果较好，修复后的数据具有良好的完整性和可信度。

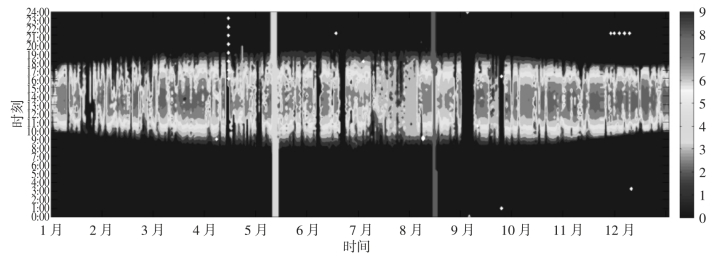
图2-9　BK光伏电站功率数据修复前功率等高线图

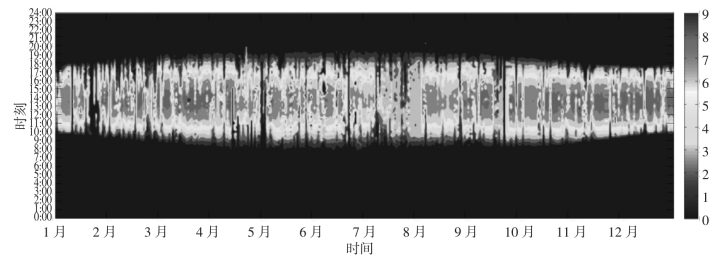
图2-10　BK光伏电站功率数据修复后功率等高线图