Σ-Δ型A/D转换原理简介

Σ-Δ型A/D转换器由Σ-Δ调制器（又称总和增量调制器）和数字抽取滤波器组成。总体框图如图8-47所示。

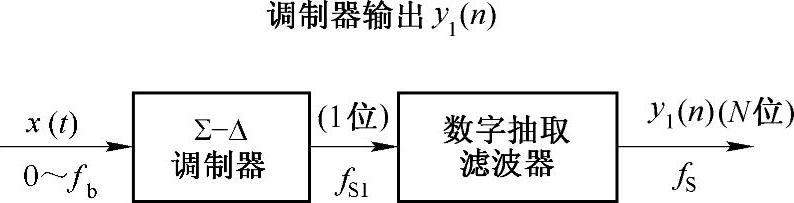
图8-47 Σ-Δ型A/D转换器总体框图

设输入带限模拟信号x（t）的最高频率为f_b，Σ-Δ调制器以非常高的采集频率f_S1对x（t）进行采样，f_S1就要比通常的奈奎斯特频率f_S（f_S=2f_b）高许多倍，常取f_S1=256f_S。Σ-Δ调制器的输出y₁（n）为1位数字信号，这种高采样频率的1位数字信号再经过数字抽取滤波器进行抽取和滤波，转换成采样频率等于奈奎斯特采样频率的高分辨率（如N=20位）数字信号，下面将详细说明Σ-Δ调制器和数字抽取滤波的原理。

1.Σ-Δ调制器量化原理

Σ-Δ调制器是一种改进的增量调制器，与传统的A/D转换器的量化过程不同，其量化对象不是信号采样点的幅值，而是相邻的两个采样点的幅值之间的差值，并把值编码为1位的数字信号输出。图8-48说明了这种量化编码的概念，图中x（t）代表输入模拟信号，时间轴按采样间隔Δt分成相等的小段，每一个Δt中，阶梯信号x₁（t）或者增加Δ或者减小Δ。只要Δt足够小，或者x（t）不是过快，那么阶梯信号x₁（t）就可以跟踪x（t）的变化，或者说阶梯信号x₁（t）就可以用来代替x（t）。因为x₁（t）在Δt间隔内的幅值变化总是Δ，所以将此变化量称为“增量”，也就是A/D转换器的量化单位。由此可将x₁（t）用1位编码来表示，当x₁（t）上升一个Δ时编码为1，下降一个Δ时编码为零，如图8-48d所示。为了能用x₁（t）来近似x（t），前提条件是Δt非常小，也就是说要求采样频率非常高。以图8-48为例，如果要想得到一个N位的A/D转换器，那么Δ=（满量程/2^N），一次转换要采样2^N次，采样时间间隔为Δt，如果采样期间共有M个1、Z个0，那么量化的数值为（M-Z），对应的信号值=（M-Z）Δ=（M-Z）×满量程/2^N。

图8-48 增量调制量化原理

图8-49是增量调制的原理图，图中x₁（t）信号经1位D/A转换而获得Δ的上升或下降由差值信号e（t）大于或小于零来决定，e（t）则由x（t）与x₁（t）经比较器得出，然后由量化编码器在采样频率f_S1控制下进行量化编码。

通常图8-49中的1位D/A转换器可用积分器来完成，同时为了改进增量调制器的高频性能，先将输入信号x（t）进行积分后再进行增量调制，从而得到图8-50所示的总和增量调制器。

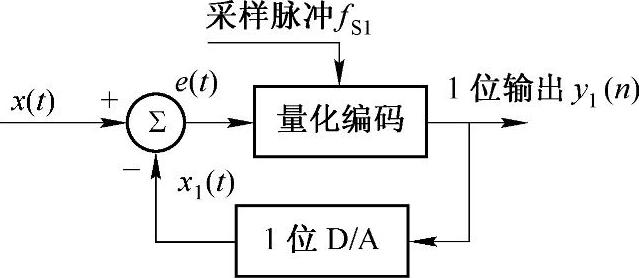
图8-49 增量调制的原理图

由图8-50可以求出输出1位数字信号y₁（n）与输入模拟信号的关系：

e（t）=∫x（t）dt-x₁（t）=∫x（t）dt-∫y₁（n）dt=∫[x（t）-y₁（n）]dt （8-24）

故有

y₁（n）=x（t）-de（t）/dt （8-25）

式（8-25）表明，除de（t）/dt项外，y₁（n）代表原始模拟信号，de（t）/dt实际上代表量化的噪声，因此将y₁（n）经低通滤波器后即可恢复x（t）。由式（8-24）还可看出，图8-50a中的两个积分器实际上可合并为一个，由此可得到图8-50b所示的简化电路。目前，大多数实际使用的Σ-Δ调制器均采用该电路。

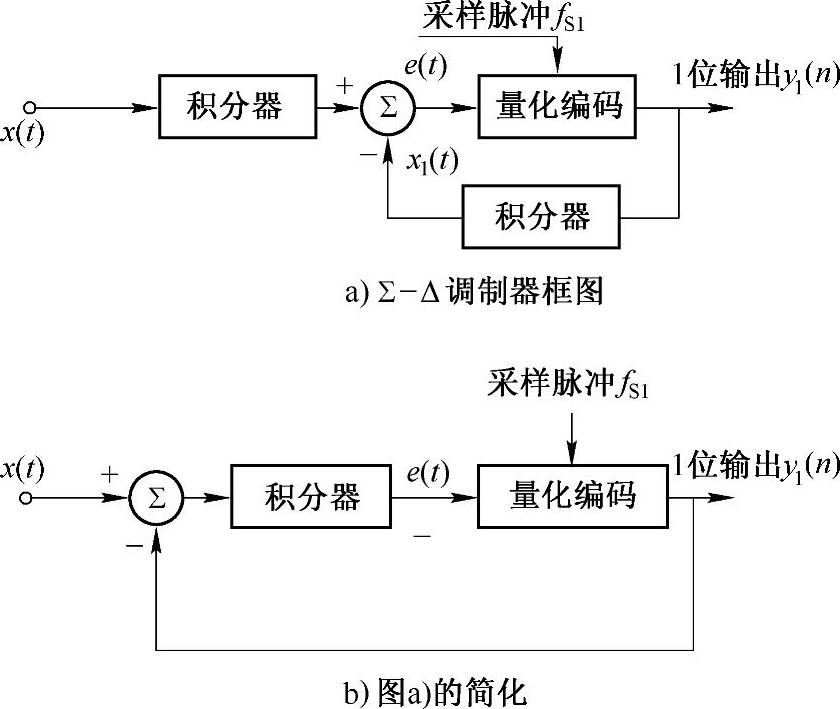
图8-50 Σ-Δ调制器电路原理图

2.量化噪声

普通幅值A/D转换器的量化噪声是由A/D转换器的位数来决定的，其量化噪声功率谱密度N₁为白噪声。

N₁=q²/12f_S1 （8-26）

式中，q=E/2ⁿ为量化电平，E为满量程电平；f_S1为采样频率；n为编码位数。显然，当n较小时，可以通过增加f_S1来减少量化噪声的功率谱密度。

Σ-Δ调制器为1位量化，n=1，但f_S1很大（常用值在奈奎斯特采样频率的256倍以上），因而其量化噪声功率谱密度同样很小。更重要的是Σ-Δ调制器对于均匀分布的量化噪声功率谱密度具有形成滤波的作用。大大减少了低频率内的量化噪声。图8-50b所示的电路图可以等效为图8-51所示的线性化领域模型。下面从频域观点给以详细分析。

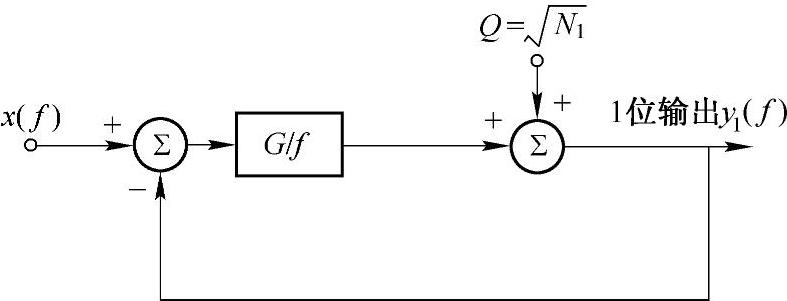
图8-51 Σ-Δ调制器频域模型(www.zuozong.com)

为了分析方便，设积分器为理想积分器，传递函数为G/f，其中G为积分器的增益，并设x（f）、y₁（f）分别为x（t）、y₁（n）的频谱，则有

y₁（f）=[x（f）-y₁（f）]G/f+Q （8-27）

式中，Q为量化噪声谱平均电平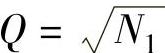

由此可得

y₁（f）=x（f）G/（f+G）+Qf/（f+G） （8-28）

式（8-28）的第一部分代表有用信号，而第二部分代表量化噪声。显然，当f=0时，y₁（f）=x（f），即为无噪声信号，随着频率增高，有用信号减小，而噪声增大；当f→∞时，有用信号趋于零，完全变为噪声。上述分析表明：Σ-Δ调制器对量化噪声进行了成形滤波，对信号表现为低通滤波，对噪声表现为高通滤波，极大地减少了A/D转换器中低频带的量化噪声，而高频段的噪声则可通过随后的数字低通滤波器去掉，从而提高了量化信噪比，其示意图如图8-52所示。

图8-52 Σ-Δ调制器噪声成形滤波

3.数字抽取滤波器

数字抽取滤波器具有数字抽取（重采样）和低通滤波的双重功能，它有3个作用：

1）低通滤波经噪声成形滤波后的Σ-Δ调制器输出噪声减至最小，其作用在图8-52中已示意表明。

2）滤除奈奎斯特频率以上的频率分量，以防止由于数字抽取产生的混叠失真。

3）进行抽取和滤波运算，减少数据率，并将1位数字信号转换为高位数字信号。

由于Σ-Δ调制器的输出y₁（n）的数据率非常高，为了减少数据率，就必须进行二次采样，将一次采样的频率f_S1降低到奈奎斯特频率f_S。降低M=f_S1/f_S倍，即进行M∶1的整数倍抽取。根据采样定理，为了防止混叠失真，在进行抽取之前，必须首先进行低通滤波，将f_S/2以上的频率分量滤除。

混叠失真是关于1/2采样频率对称的。Σ-Δ型A/D具有两次采样，对于第一次采样，由于f_S1＞＞f_b，因此，允许f_S1～f_b之间的频率分量存在，而不会因混叠失真影响0～f_b的有用频带，如图8-53所示。因此，几乎所有采用Σ-Δ型A/D转换器的前端都不需要采用抗混叠低通滤波器，但对于第二次采样，由于f_S/2已接近（或等于）f_b，所以，必须进行抗混叠低通滤波。

图8-53 二次采样与混叠失真

数字抽取滤波器的第三个作用是减小数据率的抽取与提高分辨率的滤波，这两项工作是同时完成的。为了保证输入信号的波形不失真，要求滤波器具有很好的线性相位特性；同时为了保证A/D转换器的精度要求，滤波器还必须具有较好的幅度特性。因此，Σ-Δ型A/D中的低通滤波器，一般采用具有线性相位特性的有限脉冲响应（FIR）数字滤波器。设滤波器的单位脉冲响应为h（n），n=0，…，（N-1），抽取滤波过程实际上是进行下述运算：

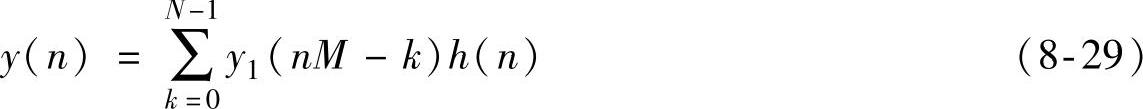
式中，N为滤波器的节数；M等于抽取比（M=f_S1/f_S）。

由于y₁（n）的取值实际仅为0或1，因此，式（8-29）实际上为累加运算。

由式（8-29）可知，经过滤波运算，A/D输出y（n）就变成了高位低抽样率的数字信号，从而实现了高分辨率的A/D转换，转换的位数实际上由数字滤波器系数的有限字长来保证。上述滤波过程可采用专用的数字集成芯片或数字信号处理器（DSP）芯片来完成。

4.Σ-Δ型A/D转换器的使用

图8-54表明了传统的A/D转换器与Σ-Δ型A/D转换器在使用上的差别。图8-54a为在采集系统中使用传统的A/D转换器，图8-54b为使用Σ-Δ型A/D转换器。二者最大的差别是：传统的A/D转换器可以多个通道模拟信号输入共用一个转换器；而Σ-Δ型A/D转换器是一个通道一个转换器，其原因在于Σ-Δ调制器是对同一信号的相邻两采样点的幅度之差进行量化的，因此，不能采用时分复用技术。此外，传统的A/D转换器每一道的前端都需一个抗混叠滤波器，而采用Σ-Δ型A/D转换器则不需要这种滤波器。