问题探究：理解抛物线性质与几何直觉探索

师：对于这个问题的具体分析我们就说到这里。下面我们再回到图8.1，来研究一下这个图隐藏着什么信息。同学们，请你们仔细观察图8.1，告诉老师你们发现了什么？

学生们认真观察图8.1，仔细探究问题，并踊跃作答。

（1）对问题提出猜想

生1：老师，我觉得图8.1中的直线QR可能也与圆O相切，也就是说圆O可能是三角形PQR的内切圆。

（2）用特殊点验证猜想

生2：我同意生1的想法，并找了一个特殊点进行验证。取特殊点P（0，－2），根据PQ、PR与圆相切求得斜率k1、k2，并求得可知QR与圆O相切。

师：嗯。很好！那同学们再想一想，是否只存在个别特殊点满足该性质，还是说对抛物线上所有的点（除x0＝±1外）都满足这个性质呢？

（3）几何直观探索问题

生3：老师，我借助几何画板进行探索发现，抛物线上所有的点（除x0＝±1外）都满足这个性质。

师：好，那请你上来给同学们演示一下。

图8.2是生3的几何画板演示图。

图8.2

生3：首先在几何画板中画抛物线y＝x2－2的图象，并在抛物线上任取一点P，过P点作圆O的切线交抛物线于Q、R两点，连接Q、R，过O点作QR的垂线交QR于点A，测得OA的长度为1 cm。当P点跑遍抛物线上（除x0＝±1外）的每一点时，始终能保持OA的长度为1 cm（等于半径的大小），所以可以得出直线QR与圆O始终相切。因此，我们可以得出结论：过抛物线y＝x2－2上（除x0＝±1外）的任意一点作圆O：x2＋y2＝1的切线，切线交抛物线于Q、R两点，连接这两点的直线始终与圆O相切。(www.zuozong.com)

（4）逻辑推理证明问题

生4：生3的方法很直观，利用几何画板从动态的、直观的角度给我们生动形象地展示了直线QR始终与圆O相切这一性质。但是从数学的严谨性角度看，这一几何直观呈现过程不能算是严格证明，所以我从代数的角度对此猜想进行了证明，证明得到的结果与生3的结论一样，下面给出我的证明思路和过程。

证明思路：要想证明过抛物线上（除x0＝±1外）的任意一点作圆O的切线，切线交抛物线于Q、R两点，连接这两点的直线始终与圆O相切，只要证明圆心O到直线QR的距离等于半径即可。

证明过程：由上述解答过程可知，kQR＝k1＋k2－2x0，Q（k1－x0，（k1－x0）2－2），可将直线设为

y＝（k1＋k2－2x0）（x－k1＋x0）＋（k1－x0）2－2，

经过化简得直线的一般方程为

（k1＋k2－2x0）x－y＋（k1＋k2）x0－k1k2－x20－2＝0。

由点到直线的距离公式知

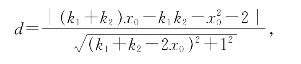
将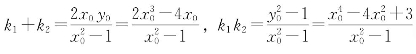代入上式得

所以，过抛物线y＝x2－2上（除x0＝±1外）的任意一点作圆O：x2＋y2＝1的切线，切线交抛物线于Q、R两点，连接这两点的直线始终与圆O相切。

同学们还在为抛物线的这一性质感到神奇，这时，下课铃声响了，教师对这节课的探讨进行了总结。

师：嗯，几位同学回答得都很好，也掌握了我们学习数学的基本规律：大胆猜想，小心论证。既从几何直观上找到了对象与对象间的关系，又从代数的角度严谨地证明了这一猜想，经过我们的探索，证明了当a＝2，r＝1时，直线QR始终与圆O相切。但这个问题还有探究下去的价值，课后请同学们再接着探索这样一个问题，对于任意给定的y＝x2－a（只考虑a大于0的情形），是否存在圆x2＋y2＝r2，当a和r满足一定的关系时，也能使直线QR始终与圆O相切呢？