
平面几何是研究平面上的直线和某些特定曲线的几何结构及其度量性质。线是平面几何最基础的元素之一,欧氏几何五大公理中就有三条与线有关。黄金分割在公元前6 世纪被古希腊数学家毕达哥拉斯发现,最早就是在线条长度上呈现出的数量关系。
相传,2 600 多年前,伟大的哲学家毕达哥拉斯在路过铁匠铺时,被清脆悦耳的打铁声吸引,凭直觉认定这声音有“秘密”!走进铺里,他仔细测量了铁砧和铁锤的比例近似值是0.618。后来古希腊柏拉图将这一比例称为黄金分割,即把一条线段AC 分为AB 和BC 两部分,此时短段AB 与长段BC 长度之比恰好等于长段BC 与整条线段AC 之比,其比值为无限不循环小数0.618 033 988……这个数叫作黄金分割数。而它的近似值为0.618,其倒数又近似为1.618。

图2-12 黄金分割示意图
更令人更惊奇的是,四千多年前的古埃及就似乎已经在应用这一规律了!胡夫金字塔塔高 146 米,底部正方形边长 232 米,两者关系为“146 ÷ 232 ≈0.629”,竟与两千年后千里之外发现的黄金分割比相差无几。毕达哥拉斯还反复验证了“黄金”长方形的存在(长方形的长和宽之比为1.618) 。
几何学里有两件宝,一是勾股定理,另一个是黄金分割。如果把勾股定理比作黄金矿的话,那么黄金分割就是钻石矿。
——17 世纪著名天文学家 开普勒

图2-13 埃及胡夫金字塔

图2-14 古希腊帕特农神庙
两千多年前,古希腊在雅典城南部修建了帕特农神庙,其正立面的长与宽之比恰为黄金分割比。而且,它的柱径、柱高与间距等也都呈现出黄金分割的完美样态,长与宽的比例大体上皆为 3 ∶5,这种严格的比例关系不仅体现了精确的技术要求,而且体现了希腊人以追求和谐为目的的审美理想。(www.zuozong.com)
人体也是世界上最美的物体之一。人体有 18 个黄金点,如脐为头顶至脚底之分割点,喉结为头顶至脐之分割点,肘关节是手指到肩部的黄金分割点,等等。
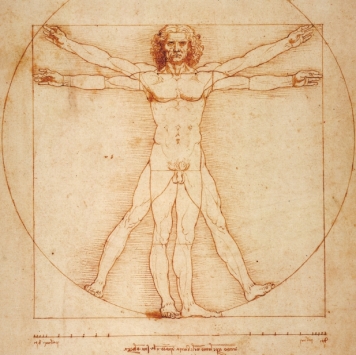
图2-15 达芬奇手稿 维鲁特人
1975 年竣工的加拿大多伦多电视塔,塔高553.3 米,而其七层的工作厅建于离地面340 米的半空,其所在高度与塔高关系为“340 ÷ 553.3 ≈ 0.615”,符合黄金分割。
自古以来,黄金分割的美被人们通过多种方式展现得淋漓尽致,它具有严格的比例性、艺术性、和谐性,蕴藏着丰富的美学价值,这一比值能够引起人们的美感,被认为是建筑和艺术中最理想的比例。这三座具有历史意义的不同时期的著名建筑——胡夫金字塔、帕特农神庙、多伦多电视塔,不约而同地用到了黄金分割比,充分证明了黄金分割比具有赏心悦目的美,能使建筑物看起来更加和谐,更加协调。

图2-16 加拿大多伦多电视塔
不仅是建筑,在艺术、生产中,几乎所有人类生活的领域里,都可以找到这个精灵的存在。优美动听的琴音,是综合了各种条件而得来的,贝多芬、莫扎特、巴赫、巴托克、德彪西、舒伯特等在他们的音乐里流淌着黄金分割的完美和谐。乐章、节中、乐曲中的大小高潮大都处在乐曲5 ∶8 的比例点上。日常休闲中,舞台报幕员在舞台上的最佳站位是在舞台宽度的0.618 之处,我们所看的高清晰度电视的屏幕长宽比多设计成16∶9。
更有趣的是,黄金分割比还能运用在生产上,成为寻求最优化方法的重要参考。1953 年,美国的基弗提出“0.618 法”,即怎样才能使产量最高、质量最好、消耗最少。如果将实验点定在区间的 0.618 左右,那么实验的次数将大大减少。实验统计表明,对于一个因素问题,用“0.618 法”做 16 次实验,就可以取得“对分法”做 2 500 次实验所达的效果,这种方法由数学家华罗庚在我国推广应用。
黄金分割的魅力得益于数,而数是万物的本原或原则,同时万物之中都存在着某种可以被人凭借理智加以认识和把握的数量关系。

图2-17 蕨类植物叶片
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




