
赵月玲1,贺朝霞1,2,宋绪丁1
(1.长安大学道路施工技术与装备教育部重点实验室,陕西西安 710064;2.江苏华通动力重工有限公司,江苏镇江 212003)
摘 要:基于离散单元法对振动筛面上颗粒流进行筛分过程的模拟研究,分析了石英砂颗粒在筛分过程中的运动状态和四层筛的筛分效率动态变化规律以及筛面倾角、振动方向角、振动频率3种结构参数对筛分效率的影响。结果表明:振动筛四层筛面的筛分效率由第一层至最后一层逐渐降低;当振动频率一定时,随着筛面倾角以及振动方向角的增加,筛分效率普遍呈现先增大后减小的趋势;当振动方向角以及筛面倾角一定时,筛分效率随着振动频率的增加呈现逐渐减小的趋势。通过本文获得的影响规律对于振动筛的快速设计具有一定的指导作用。
关键词:离散单元法;颗粒流;筛分;结构参数;效率
Abstract:Based on Discrete Element Method(DEM)the screening process of particles flow on the vibrating plate is simulated.The motion state and efficiency change of four-layer screens were analyzed for quartz sand particles flow.Then the influence of inclination of screen surface angle,vibrating direction angle and vibration frequency on screening efficiency were discussed.The results show that the screening efficiency of four-layer screen is gradually reduced from the first screen to the last one.With the increase of the inclination of screen surface angle and vibrating direction angle,the first increasing and then decreasing tendency of screening efficiency is obvious when the vibration frequency is constant.And with the increase of the vibration frequency,the decreasing tendency of screening efficiency is obvious when the inclination of screen surface angle and vibrating direction angle are constant.The method proposed in this paper can improve the efficiency of design for the vibrating screen.
Key words:DEM;Particles flow;Screen;Structure parameter;Efficiency
1 引言
筛分作业在诸如冶金、煤炭、化工、医药等行业中是一个重要的生产环节,它是将松散的混合物料,通过单层或多层面的筛孔,按照粒度将其分成2种或若干种不同粒度级产品的过程[1]。筛分效率是动态变化的,寻找振动筛的最佳运动学参数,能够提高筛分效率,延长筛分机械和筛面的使用寿命。对于各类筛机来说,筛面倾角、振动方向角以及振动频率等参数对筛分效率均有直接影响[2-3]。
本文基于离散单元法[4]对振动筛面上颗粒流进行筛分过程的模拟研究,通过多组试验选择最能够反映出物料颗粒在筛面上运动的真实情况的参数。通过模拟计算出当筛面倾角以及振动方向角分别不同时四层振动筛面的筛分效率。
2 模型建立与计算流程
2.1 颗粒模型与颗粒接触模型
离散单元法把分析对象看成充分多的离散单元,每个颗粒为一个单元,根据全过程中的每一时刻各颗粒间的相互作用计算接触力,再运用牛顿运动定律计算单元的运动参数,这样交替反复运算,实现对象运动情况的预测[5]。
颗粒模型中的颗粒运动是相互独立的,只有当发生接触时才会在接触点处产生相互作用。颗粒的离散性使得它在受载和不受载的情形下会产生复杂的运动。最常用的颗粒模型是把颗粒看做圆盘或球体,即二维刚性圆形颗粒模型和三维刚性球形颗粒模型[5]。如图1所示为颗粒接触模型[6]。
作者简介:赵月玲(1991-),女,长安大学工程机械学院硕士研究生,机械制造及其自动化。
贺朝霞(1978-),女,长安大学工程机械学院副教授,研究生导师。
宋绪丁(1963-),男,长安大学工程机械学院教授,博士生导师。
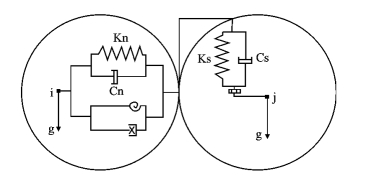
图1 颗粒接触模型
根据颗粒接触模型,颗粒在运动过程中主要受其自身重力和颗粒间的法向及切向碰撞接触力作用,同时,颗粒还受到2种力矩的作用,即切向力造成的力矩和滚动摩擦力矩[6]。因此第i个颗粒的运动方程[6]可由公式(1)和(2)表示。
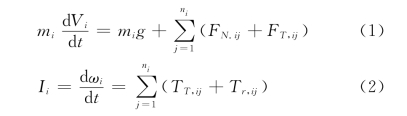
其中,m和I分别表示小球的质量和转动惯量,ni表示与小球i接触的颗粒总数,V表示移动速度,ω表示角速度,t表示时间,g为重力加速度,FN,ij和FT,ij分别表示法向作用力和切向作用力,TT,ij和Tr,ij分别表示切向力矩和滚动摩擦力矩。
2.2 筛分效率计算方法
筛分效率是筛分时实际得到的筛下产物的重量与入筛物料内所含小于筛孔尺寸的粒级重量之比。目前采用的振动筛筛分效率的计算方法主要有行业标准计算方法和汉考克公式计算方法。在沥青搅拌设备的筛分中,根据行业标准JT/T2702-2002多层振动筛筛分某段时间后计量出试样通过量与试样总质量的比值,但是这种计算方法没有考虑振动筛中各层筛面筛上物与筛下物物料粒级混杂分布的情况。在煤炭行业通常采用汉考克公式[1],这种方法国际上较为通用且考虑到了筛网混杂粒级分布的情况,但是采用汉考克公式时,很难测定各层筛面筛上物物料、筛下物物料的重量以及粒级百分比这些参数。
在测定筛分效率的过程中,由于试验成本高,无法频繁变换参数进行仿真,所以需要采用基于离散单元法的颗粒动力学软件EDEM来模拟筛分过程。
本文所采用的筛分效率计算方法流程如下:首先对振动筛进行初步设计,主要采用自编的matlab程序获得基本的工艺参数。然后根据初步设计的结果,进行详细结构设计获得振动筛的三维模型,从而获得较为准确的结构参数。同时,根据初步设计对筛分系统建立集中质量法的动力学模型,获得各结构部分响应,以及精确振幅、振频等参数。
然后将系统动力学和三维模型的输出结果作为离散单元法EDEM软件分析的输入,建立合理的颗粒动力学模型,完成筛分过程的分析。进一步获得筛分后各个筛面上下的不同粒度物料的组成比例,最后得到第i层筛网的筛分效率,效率计算根据汉考克公式进行计算。

3 颗粒动力学分析
3.1 颗粒动力学分析设置
颗粒动力学分析设置中的材料属性参数以及材料接触属性参数列于表1中。石英砂属石性物料,材料属性与石料相近,所以取石料代替。在理想的情况下发生完全弹性碰撞,在这个过程中没有热传递、没有静电力等,只有机械能之间的相互转化,所以表中所有材料的静电力都是0。
表1 材料属性及材料接触属性

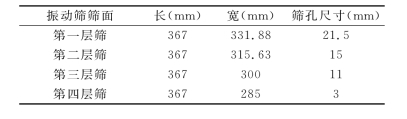
本文所采用的振动筛侧面模型图如图2所示(其中α为筛面倾角,δ为当振动方向线为水平时的振动方向角),各层筛面的尺寸如表2所示。
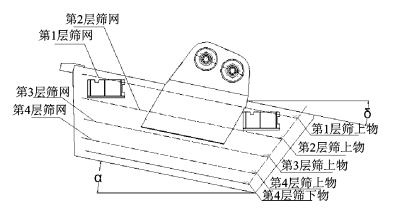
图2 振动筛侧面模型图
表2 振动筛模型各层筛面的尺寸
所采用物料不同粒级的比例及其质量如下:粒级为22~25mm的物料的质量占总体的8%,为0.01kg;粒级为15~21mm的物料占总体的20%,为0.025kg;粒级为11~14mm的物料占总体的14%,为0.017kg;粒级为3~10mm的物料占总体的31%,为0.038kg;粒级为<3mm的物料占总体的27%,为0.034kg。在1s的筛分过程中,物料在振动筛周期力的作用下不断被抛掷,使得大小颗粒之间形成分层,比筛孔尺寸小的颗粒发生透筛形成筛下物,比筛孔尺寸大的颗粒继续留在筛面上。
图3所示为颗粒物料筛分的三维离散元法模拟过程。随着入料的增多和筛分过程的进行,筛面上的颗粒逐渐形成颗粒流,大小颗粒之间不断发生分层,未透筛的小颗粒以及不能透筛的大颗粒继续在筛面上运动,当筛分即将结束时,不同筛面上的物料颗粒大小明显不相同,越靠近上层的物料颗粒越大,越靠近下层的物料颗粒越小。
3.2 仿真结果分析(www.zuozong.com)
3.2.1 筛面倾角对筛分效率的影响
采用两组实验进行仿真模拟,第一组的振动方向角均为30°,第二组的振动方向角均为35°,两组的频率均为16.7Hz。仿真模拟后的筛分效率见表3。
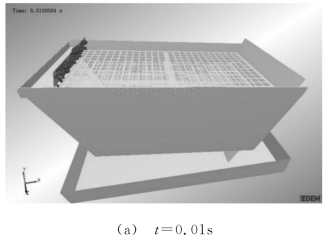
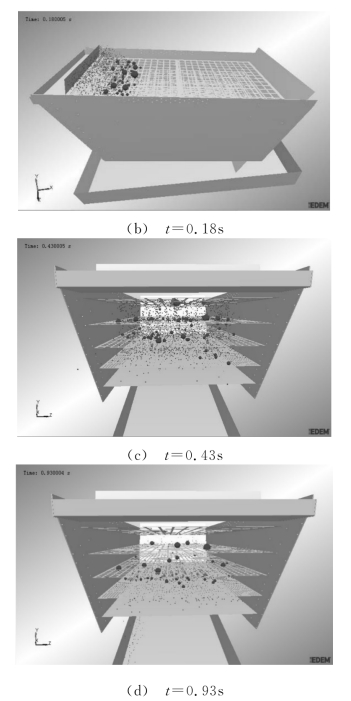
图3 颗粒物料筛分过程模拟
表3 筛面倾角对筛分效率(%)的影响
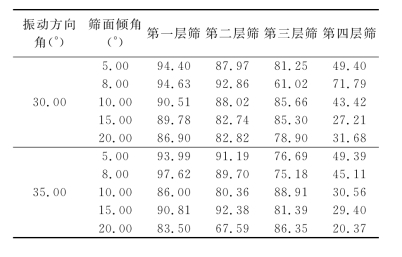
根据表3的数据拟合出筛面倾角与筛分效率关系曲线图,如图4。根据表3和图4可以知道,对于给定参数的振动筛,为了使振动筛筛分效率控制在一个比较理想的范围内,应将振动筛倾角控制在一定范围内。振动筛倾角超过10°以后,且其效率下降较为明显,主要是由于倾角增大,颗粒流动速度增大,不同粒级颗粒互相裹挟未经透筛就进入了料仓,因此降低了筛分效率。
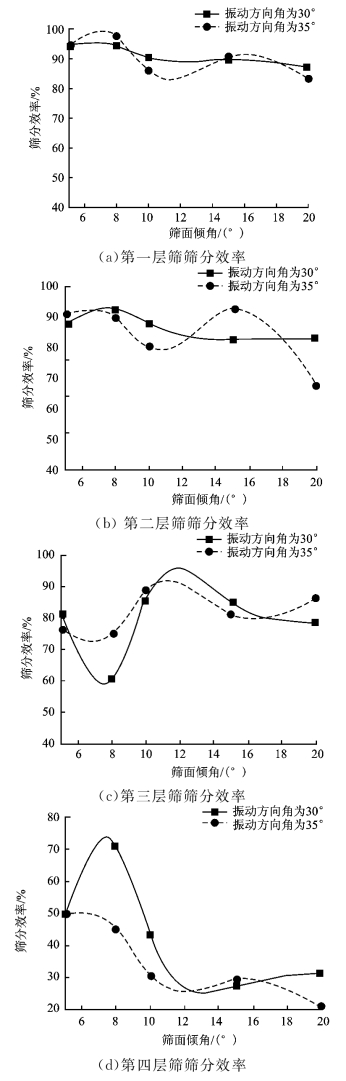
图4 筛分效率与筛面倾角关系曲线图
3.2.2 振动方向角对筛分效率的影响
采用两组实验进行仿真模拟,第一组的筛面倾角均为12°(在研究筛面倾角对筛分效率的影响中,12°是当前研究的一个临界值),第二组的筛面倾角均为10°,两组的频率均为16.7Hz。仿真模拟后的筛分效率见表4。
表4 振动方向角对筛分效率(%)的影响
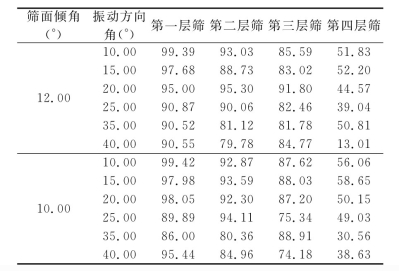
根据表4中的数据拟合出振动方向角与筛分效率关系曲线图,如图5。从表4和图5可以知道,当振动方向角超过30°度以后,各层效率下降较为明显。在振动方向角增大初始阶段,物料每次抛掷运动所移动的距离越短,保证了物料在筛面上充分透筛。但随着振动方向角进一步增大,筛面上较厚的料层不能沿筛面全长充分分层和透筛,使得筛分效率降低。
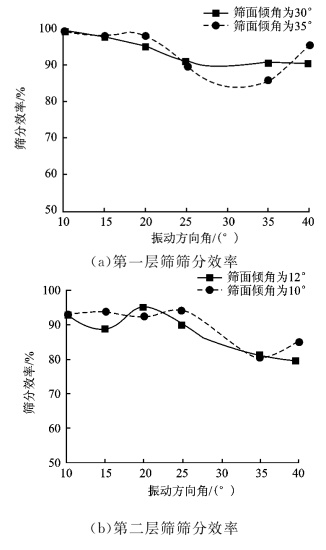
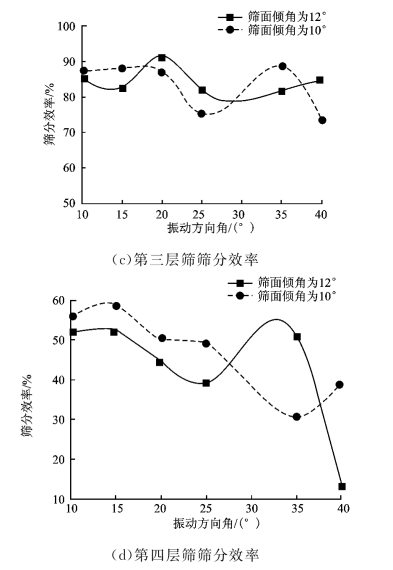
图5 筛分效率与振动方向角关系曲线图
3.2.3 振动频率对筛分效率的影响
采用两组实验进行仿真模拟,第一组的振动方向角均为30°,第二组的振动方向角均为35°,两组的筛面倾角均为10°。仿真模拟后的筛分效率见表5。
表5 振动频率对筛分效率(%)的影响
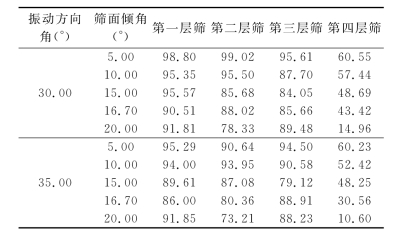
根据表5中的数据拟合出振动频率与筛分效率关系曲线图,如图6。根据表5和图6可以知道,给定参数的四层直线振动筛,当振动频率超过15Hz后,各层筛分效率均有降低,尤其第四层时,细颗粒的筛分效率下降明显。主要是由于频率过大后,物料抛掷速度增大,处理能力获得提升。但部分颗粒未来得及与筛面接触就进入料仓,使得筛分效率降低。
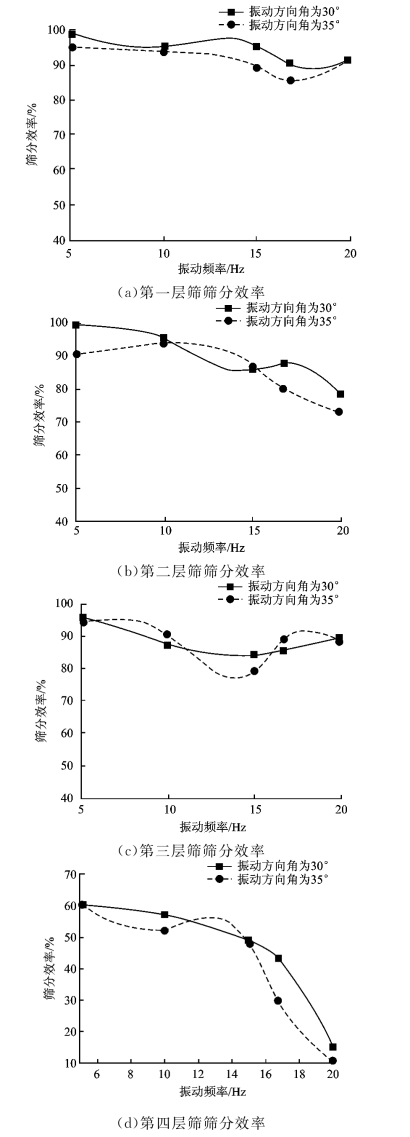
图6 筛分效率与振动频率关系曲线图
4 结论
在沥青搅拌站的振动筛效率计算中,为了降低采样现场试验的成本,考虑基于离散单元法来进行颗粒动力学分析,精确地模拟并预测筛分中物料的运动过程。本文通过分析筛面倾角、振动方向角以及振动频率3个参数对多层振动筛筛分效率的影响,得出以下结论:
(1)采用离散单元法能够对球形颗粒的直线振动筛筛分过程进行模拟仿真研究,通过设计几组不同筛面倾角以及不同振动方向角的仿真实验,可以得到物料在筛面上的运动状态以及不同层筛面的筛分效率。
(2)随着入料的增多和筛分过程的进行,筛面上的颗粒逐渐形成颗粒流,大小颗粒之间不断发生分层,未透筛的小颗粒以及不能透筛的大颗粒继续在筛面上运动,当筛分结束时,各层筛面上各粒级的物料比例发生明显变化,随着层面的不断向下,粒级大的物料比例逐渐降低,粒级小的物料比例逐渐增大。
(3)筛分效率随着筛面倾角的增大有一个先增大后减小的过程。在一定范围内,倾角增大,筛上物料的抛掷强度会增大,物料在筛面上向前的运动速度就会加快,从而使振动筛的处理量提高。但是倾角过大,会使得物料在筛面上停留的时间缩短,与筛孔尺寸接近颗粒的透筛机率将会减小,也就降低了筛分效率。
(4)筛分效率随着振动方向角的增大先增大后减小。在振动方向角增大初始阶段,由于振动方向角越大,物料每次抛掷运动所移动的距离越短,能够实现物料在筛面上充分透筛。但振动方向角进一步增大使得筛面上较厚的料层不能沿筛面迅速输送,各粒级颗粒间互相裹挟被送入筛上物,无法充分分层和透筛,使得筛分效率降低。
(5)当超过一定振动频率后,筛分效率开始降低。主要是由于振动频率对颗粒在筛面上的跳动状态影响很大,随着振动频率的增大,物料在筛面上的运动速度将会变大,这使得物料与筛面的接触时间减少,颗粒未来得及透筛就进入了料仓,筛分效率便出现了降低。
参考文献
[1]严峰.筛分机械[M].北京:煤炭工业出版社,1995,1-7.
[2]朱允言,孙乐殿.直线振动筛的生产率和筛分效率[J].北京科技大学学报,1991,13(1):71-77.
[3]张路霞,李云峰.振动筛筛分效率的影响因素分析[J].煤矿机械,2008,29(11):74-76.
[4]王国强,郝万军,王继新.离散单元法机器在EDEM上的实践[M].西北工业大学出版社,2010,1-4.
[5]胡国明.颗粒系统的离散元素法分析仿真[M].武汉:武汉理工大学出版社,2010:7-10.
[6]赵啦啦,刘初升,闫俊霞,等.振动筛面颗粒流三维离散元法模拟[J].中国矿业大学学报,2010,39(3):414-419.
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




