电磁波在各向同性介质中的复矢量波动方程

首先求出波动方程在媒质中的瞬时值的表示式，然后再求出波动方程复矢量形式的表示式。为了求出波动方程，需要引入一个算子∇2，称为拉普拉斯算子（Lapalace，法国数学家），当算子作用于标量函数u 时，例如，∇2u=∇·∇u表示先求u 的梯度，再求梯度的散度；当∇2作用于矢量函数A 时，∇2A 要按照数学中给出的关于∇2A 的定义式（称为矢量恒等式）来进行运算，即

式中，等号右边第一项表示先求A 的散度，再求散度的梯度；第二项表示对A 的旋度再取一次旋度。在直角坐标系中∇2A 为

式中，x、y、z 分别为沿三个坐标轴正方向的单位矢量，Ax、Ay、Az为A 在三个坐标轴上的投影。但是，只有在直角坐标系中才能将2∇A 表示为各个分量的和的形式，而在其他坐标系中就不可能写成这种简单的形式，而应根据定义式对2∇A 进行运算。

（一）波动方程在媒质中的瞬时值表示式

根据式（2.1-29）已知

对等号的两边取旋度

根据式（2.1-30）并假设在所讨论的区域内J=0，则

这样，

即

根据式（2.2-1）并假设在所讨论的区域内ρ=0，即∇·E=0，则

由此得

同理，对于

经过类似的推导过程可得

式（2.2-3）和式（2.2-4）中的第一项表示场量对空间坐标求二次偏导，即场量对于空间坐标的变化，第二项是场量对时间求二次偏导，即场量对于时间的变化，也就是说，方程将场量对于空间坐标的变化与它对于时间的变化紧密地联系在一起，因此把方程称为矢量形式的波动方程（在媒质中的波动方程）。这两个方程对于场量随空间坐标和时间的任意变化规律都是适用的。

（二）复数形式的麦克斯韦方程

如同在第1章中曾讲过的，对于随时间的变化规律是简谐函数的电压波和电流波用复数表示法会给运算带来方便，同理，对电磁场而言也是如此。对于时变电磁场，它是空间坐标和时间的函数，有四个变量，在一般情况下，对场方程直接求解比较困难。但是，当场量随时间的变化规律是简谐函数时，可以将场量随空间坐标的变化和它随时间的变化分开来讨论，因此，若采用复数表示法就更显得简便，对场方程的求解也会变得比较容易。由此可见复数形式的麦克斯韦方程在解决电磁场问题中的重要性。

对于时变电磁场，各个场量都是空间和时间的函数，而其随时间（t）的变化规律可以是任意的。例如，以电场E 为例，若选取直角坐标系（x，y，z），则可将E 表示为三个分量相加的形式：

式中的x、y 和z 分别为沿x、y 和z 轴正方向的单位矢量，Ex、Ey和Ez分别为E 在x、y 和z坐标轴上的投影，即E 在各坐标轴上分量的幅值。对于其他场量也可以写出类似的表示式。但是，正如在第1章中曾指出的，经常遇到的是随时间的变化规律为简谐振荡的场，因此本章和本书只讨论简谐场的情况。当电磁波的波源是具有一定角频率ω 的简谐场时，则在线性媒质中，在稳定状态下所激发的场量是与波源具有同样角频率的简谐场。对于这种场量，采用复数表示法是比较方便的，这样，就得到了简谐矢量场的复数表示法——复矢量（具有大小、方向和初相角的量）。例如，仍以电场E 为例，其瞬时值可表示为(www.zuozong.com)

式中，φx、φy、φz为各分量的初相角，这些量仅是空间坐标（x，y，z）的函数，为书写方便，以后均省写了坐标变量。现采用复数法（复矢量）来表示式（2.2-6）的电场E；为了与场量随时间的变化规律可以是任意的情况区别开来，同时也为了与一般的复数和一般的实数矢量相区别，暂时在场量的符号上加一个圆点“·”，用以表示复矢量。这样，式（2.2-6）即可写为

或简写为

式中

式中的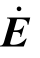为

称为电场E（x，y，z，t）的复矢量。在上式中，是的分量的复振幅，而Ex、Ey、Ez则称为相应分量的振幅。

对于随时间做简谐规律变化的磁场H（x，y，z，t），则可用磁场的复矢量表示为

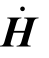式中的为

依此类推，在简谐场的情况下，其他的场矢量（如D、B 和J 等）也都有与其相对应的复矢量。顺便指出，在上述表示式中采用的符号是Re（取实部），显然，也可采用Im（取虚部）。另外，需要说明的是，虽然可以将电场复矢量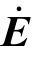或磁场的复矢量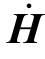写成其在三个坐标轴上的三个分量相加的数学表示式，但是却无法用空间的图形把它表示出来，因为每个分量都有自己的初相角（xφ、yφ 和zφ），而且就一般情况而言，这三个初相角是各不相同的。这正是复矢量与一般的实数矢量不同之处。

以上所讲，是场矢量在直角坐标系中的表示方法，至于在其他坐标系中的表示方法，与此相类似，所不同的只是坐标变量与单位矢量因坐标系不同而异。

应特别指出的是，因为本书所讨论的都是简谐场，为了书写方便，在以后的讲述中，复矢量符号上的小圆点“·”均省略。但是应记住，除特别指出者外，它们都是复矢量，而不是瞬时值，切不可因为两者的字母符号相同，而把它们的不同含义混淆了。根据这个约定，就可以从式（2.1-29）～式（2.1-33）得到以复矢量表示的麦克斯韦方程组为

经过以上的运算过程，把表示场量之间瞬时关系式的麦克斯韦微分方程变成了用复矢量表示的麦克斯韦方程，需要注意的是，该方程中的场量只是空间坐标的函数，不再含有时间变量t，因为在上述的运算过程中已将时间因子消除了。在实际问题中应首先对复矢量的麦克斯韦方程求解，得到场量随空间坐标变化规律的具体表示式，然后再利用场的复矢量表示法与场的瞬时值之间的关系式，就得到了场量的完整的表示式，即场量在所讨论区域内的空间分布状态以及它随时间的变化情况。

（三）复矢量形式的波动方程

已知电场E 和磁场H 的复数表示式分别为式（2.2-7）和式（2.2-9），将它们代入式（2.2-3）和式（2.2-4）中，经运算可得

令

则有

这就是用复矢量表示的在无源区域的波动方程。式中，，λ 是角频率为ω 的电磁波（TEM 波）在无界媒质中的波长，v 是波在媒质中的传播速度，K 称为相移常数，也称为波数（1/λ 为单位距离上的波长数，称为波数，但一般地，把它的2π 倍，即2π距离上含有的波长数2π/λ 称为圆波数，简称波数）。这是两个复矢量形式的波动方程，也称为齐次的亥姆霍兹方程（Helmholtz，德国物理学家），它对任何坐标系都是适用的，但是，正如前面已讲过的，在非直角坐标系中，∇2E 和∇2H 的表示式比较复杂，其原因在于，在直角坐标系中沿坐标轴方向的单位矢量是不变化的（常矢量），而在其他坐标系中沿坐标轴方向的单位矢量不是常矢量，是变化的，因而表示式也较复杂。

电磁波在无界媒质中的传播速度，在自由空间（近似地讲，在空气中）的速度。