常用有限元分析类型在工程CAE中的应用

1.弹塑性分析

结构的应力在它的值达到材料的屈服点以前，与载荷存在比例关系，载荷除去的话就回到原来的形状（初应力状态），这一时期称为处在线弹性应力状态。如构件变形继续进行，应力一过屈服点，就成为塑性状态，即使除去载荷，它的形状也不能完全回到原来的样子。有关拉伸试验和应力—应变关系，如图3-32所示。

线性应力分析是在弹性范围内的分析，弹塑性分析则是超过材料的弹性范围的分析。弹塑性分析对分析棒和板的塑性变形、塑料成型和锻造、试验棒的拉断等场合是有必要的。一般进行机械结构设计时，应力设计在弹性范围内。受到载荷的状态，应力是不是落在弹性范围内的验证，可用弹性应力分析。但是，像求机械结构的载荷承受值，如考虑塑性变形的情况，就必须要用非线性有关的弹塑性分析。

作为输入数据所必需的项目，对于材料的物理特性必须输入应力—应变关系（也可用剪切刚度），硬化准则、屈服条件和屈伏点。在非线性分析中，不是一下子就加上达到目的所在的全部载荷，为了使载荷慢慢地增加，必须输入载荷的增量值（也称为时间增量）。另外在加多个载荷时，要设置加这些载荷的顺序。和线性的应力分析相同，可使应力、位移、应变输出，在塑性区域内，屈服应力成为最大应力。作为评价的项目，有载荷和位移的关系（P—δ关系）、载荷和应变的关系、屈服区域的扩展、变形和应变的进展等。

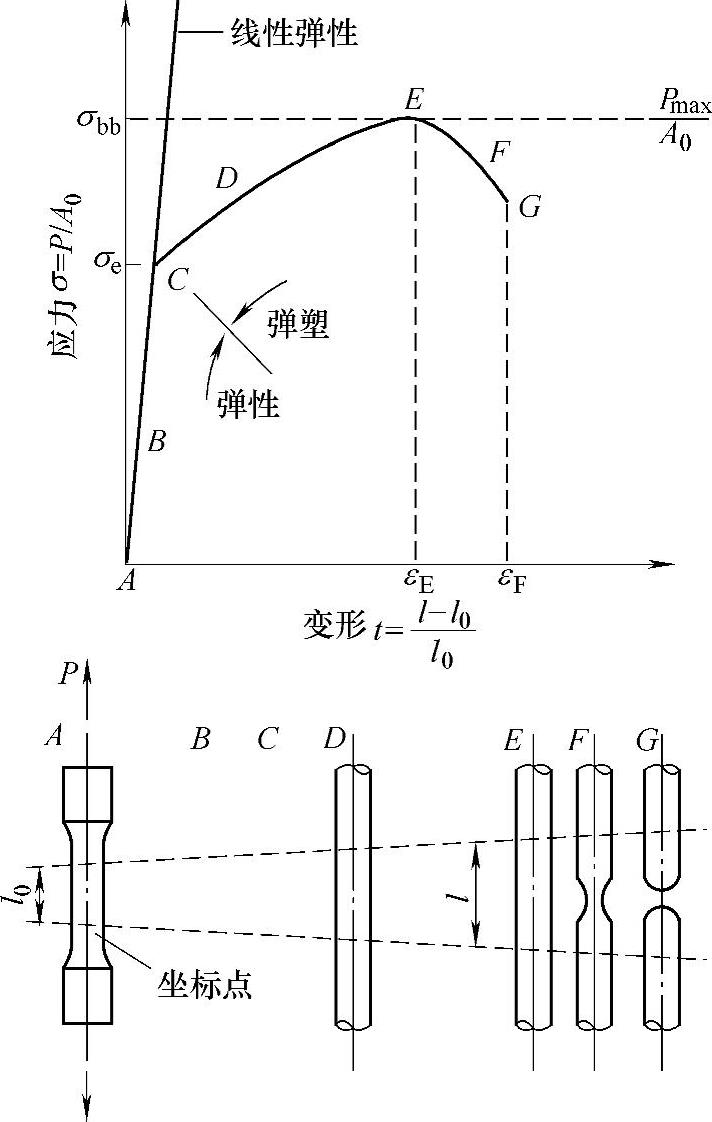
图3-32 拉伸试验和应力—应变关系

2.超弹性分析

超弹性的性质包括应力和应变的关系，如图3-33所示的不是直线，并且还有大应变，卸载时沿着加载路径的反向返回，载荷回到0，则应变（变形）也为0。变形返回原来的样子这一点来说是弹性的，而纵弹性模量所依赖的应变这一点上却是非线性。这样性质的材料的分析用超弹性分析，多数场合伴随着大变形或大应变。

橡胶材料是超弹性材料中的一种，这种场合泊松比为0.5（非压缩材料）或者在其附近。用橡胶材料制成的O型环、垫圈、衬套、密封垫和轮胎等，在处理大变形的场合，都利用大变形、大应变等性能。即使金属由于应力的有或无内部结晶结构会发生变化，由它的大变形、大应变度可达到超过10%，而仍持有超弹性性质。

分析的执行顺序与线性分析相同，但需用材料物理性质输入超弹性材料的特性。根据需要指定考虑大变形或大应变，由分析得到应力、位移和应变等。

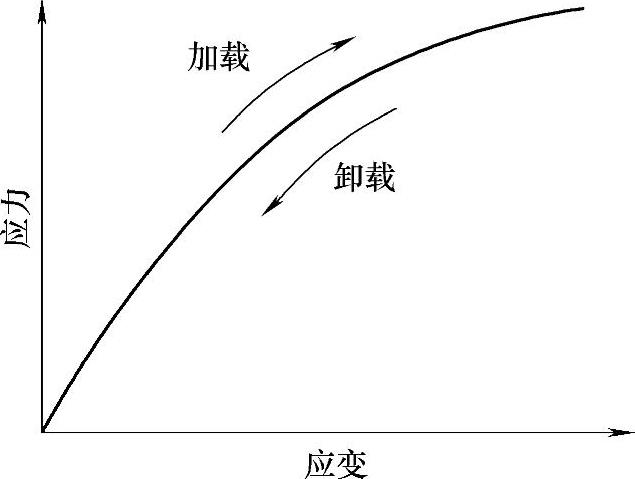
图3-33 应力-应变线图

在CAE软件中具有定义点对点、线对线以及面对面接触的功能。所谓线是连接几个节点的二阶曲线，所谓面则是由多个板单元的面所形成的三阶面。根据需要可以分别表示一阶接触、二阶接触、三阶接触。最基本的接触功能是节点与节点的接触功能，定义两点间的非线性弹簧，来模拟接触现象。将把这种非线性弹簧节点间距离作为参数，在节点离开某个一定的距离以上时，弹簧的刚度为0，而近到这以内的距离很快就成为弹簧的高刚度。此时，定义了太高的刚度值的话，整个模型的刚度平衡就要变坏，分析的精度因而就会下降。反之，因定义了太软的弹簧刚度，就要陷进对方中去，不成为接触问题了。

线接触和面接触要用与以上所不同的考虑法。对于想要定义接触的相对的线和面，分别要定义好主线和主面或从线和从面。常用在边检查是不是接触到对方边将分析进行下去。判断到变形进入接触，便在那里用它产生的反力来模拟接触。像橡胶材料那样自身的变形很大，发生自己接触自己那样的情况，在CAE软件中也有对自身接触自身进行判断的软件平台。

3.屈曲分析和特征值分析

这里说明一下有关屈曲分析和特征值分析的步骤，可以用与应力分析一样的步骤来形成模型。但是在一些步骤中所设置的内容有所不同，这里比较这三种的分析步骤，并说明它们的不同之处。

屈曲分析中载荷设置是关键。在进行屈曲分析时，和应力分析中采用一样的步骤来划分单元，设置单元、材料特性，设置约束条件、载荷条件。但是在载荷条件中所设置的载荷是以相对于屈曲载荷而言的基本载荷而设置的，而且用来设置的载荷如果设置成单位载荷（1kgf、100kgf、1000kgf、1tf等）的话，通过使用输出结果的屈曲特征值，能够容易地算出屈曲载荷。

屈曲分析的分析结果（输出资料）不是位移，而是屈曲模态、屈曲特征值。即使对于屈曲分析，同样地屈曲模态相当于应力分析中的位移，输出的话则将屈曲特征值和屈曲模态成对地进行输出。用户为了知道屈曲的临界载荷可以利用这个分析，屈曲载荷也可得到。在屈曲分析中，设置的载荷条件可以使用单位载荷来设置。用户可以根据输出的屈曲特征值资料能够知道临界的屈曲载荷，屈曲载荷=单位载荷×屈曲特征值。

特征值分析一定要有质量。在进行特征值分析的时，有关质量的数据（质量或密度）是一定要有的。载荷的概念，即进行载荷模型化处理或进行设置在这个分析中是不需要的。在执行求解的时候，根据系统的不同也要选择求解方法（求解固有振动分析的方法）。一开始的时候就用系统标准设置的分析法（默认设置），所要求的内容除了分析方法的类型外，还有选取固有频率的范围（如：1000～5000Hz），所指定范围内的特征值的个数（如：3个）等。

另外，特征值分析的分析结果（输出资料）不是位移而是固有振动模态和固有频率。在特征值分析中，固有振动模态相当于应力分析中的位移，输出资料则为成对地输出固有频率和振动模态。特征值分析中一定要有与质量有关的数据。另外，载荷条件的设置在特征值分析中是不需要的。质量是材料特性数据之一。即使在应力分析中，对于自重分析或受到惯性力的问题，质量数据也就一定要有了。系统里如果在材料特性中设置了质量的话，则使用其他载荷条件的设置中所定义的加速度资料可以自动地设置好载荷条件。加速度的资料则在其他载荷条件设置中进行定义，屈曲分析的基本步骤如图3-34所示。下面对三种分析方法进行简单说明。

（1）应力分析 图3-35所示，构件一端固定，求另一端以1lbf力拉伸时的变形和应力为例，形成FEM模型的步骤因所使用的前后处理程序的不同，而有所不同。这里以如下所示的方式来进行。材料的物理数据：弹性模量为2.9×10⁷lbf/in²，泊松比为0.32，板厚t=1。

图3-34 屈曲分析的基本步骤

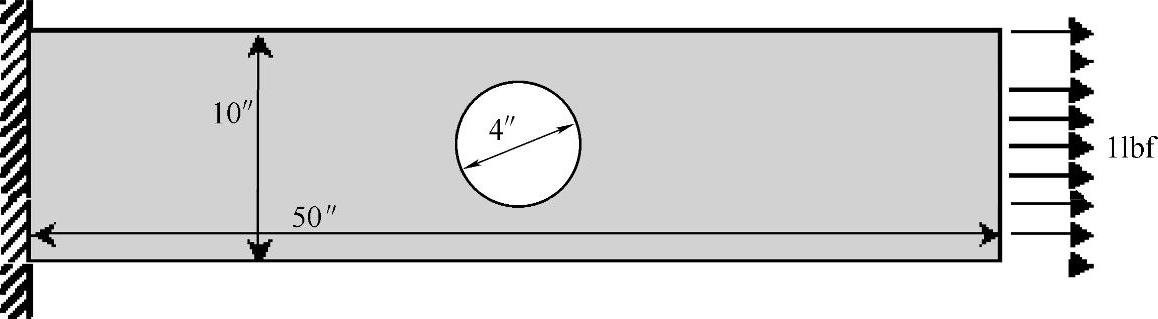
图3-35 构件拉伸

（2）屈曲分析 构件固定住一端，求另一端以1lbf力压缩的情况的屈曲载荷和屈曲模态。形成FEM模型的步骤，因所使用的前后处理程序的不同而有所不同。这里以如图3-36所示的步骤来进行。

（3）特征值分析 一端固定时的构件从低阶开始的3个固有频率和固有振动模态。形成FEM模型的步骤，因所使用的前后处理程序的不同而有所不同，主要是分析的类型和材料特性要求，需要材料的密度等特性。这里如以下所示的那样来进行。材料的物理数据：弹性模量为2.9×10⁷lbf/in²，泊松比为0.32，板厚t=1，密度3.548lb/in。

对如图3-37所示的轴对称塑料瓶加上峰值载荷，并使瓶子处于能排气的状态，注意不是抽真空。将它直立在水平面上，对着处在水平位置的瓶盖来压缩瓶子。瓶盖就有一定的速度，对瓶子本身、瓶子和水平面、瓶子和瓶盖的接触状态进行定义。这个典型的分析包括特征值分析、屈曲分析、大变形分析。其求解的应力、应变和位移输出结果如图3-36～图3-39所示。

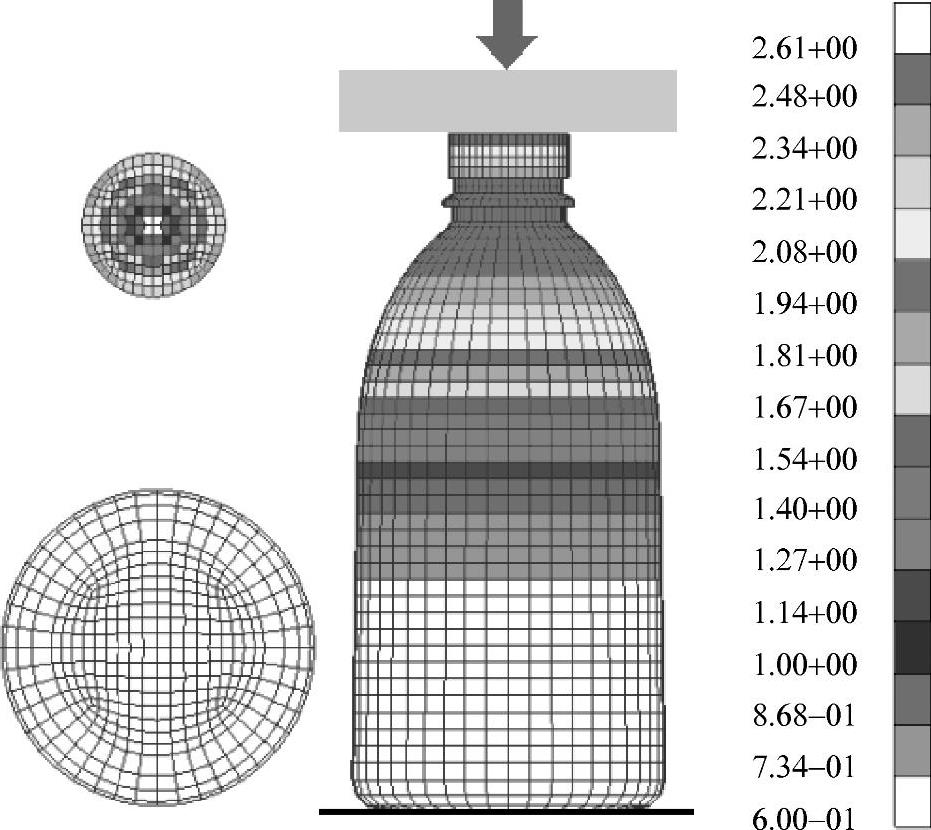
图3-37 瓶子形状以及瓶壳受压部分

图3-36 屈曲分析

4.大变形分析

（1）概要 大变形分析是一种用于由载荷而产生了的应变小变形大，或者变形即使小但伴随着变形刚度变化很大时的分析，也是一种对变形后的形状，计算力的平衡的所必需的应力分析。典型示例如图3-41所示，大变形虽然是一种非线性分析，然而以材料力学来看因为是弹性范围内的变形，所以撤回载荷的话就会回到原来的形状。一边使载荷分阶段性地增加，一边进行分析，分析中也会出现屈曲现象。非线性屈曲分析与线性屈曲的特征值分析不同，它也可求出屈曲后的变形和应力。

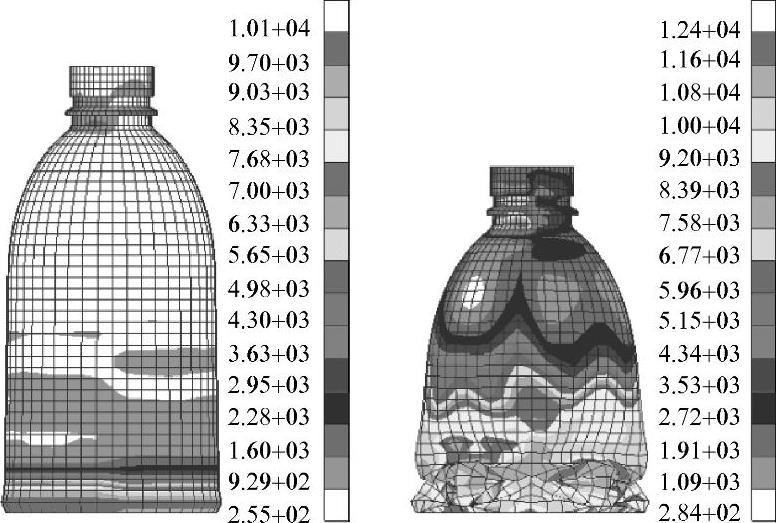
图3-38 变形及等应力分布

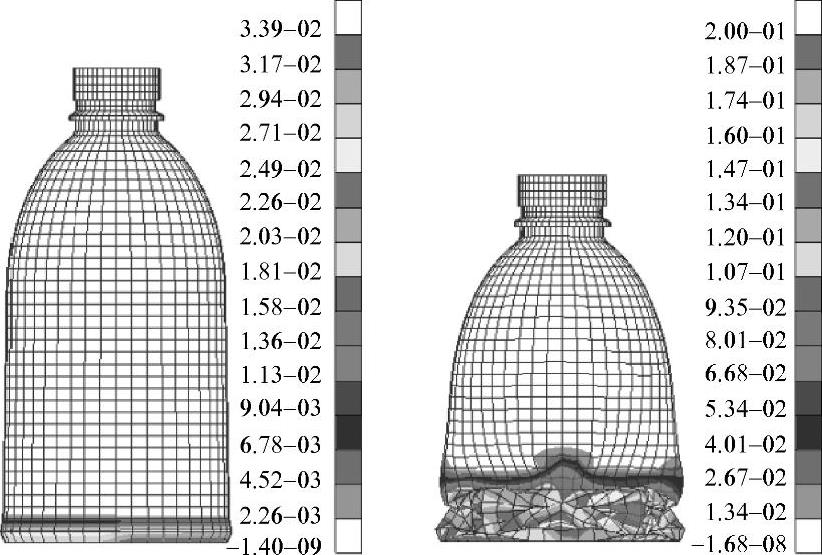
图3-39变形和塑性应变

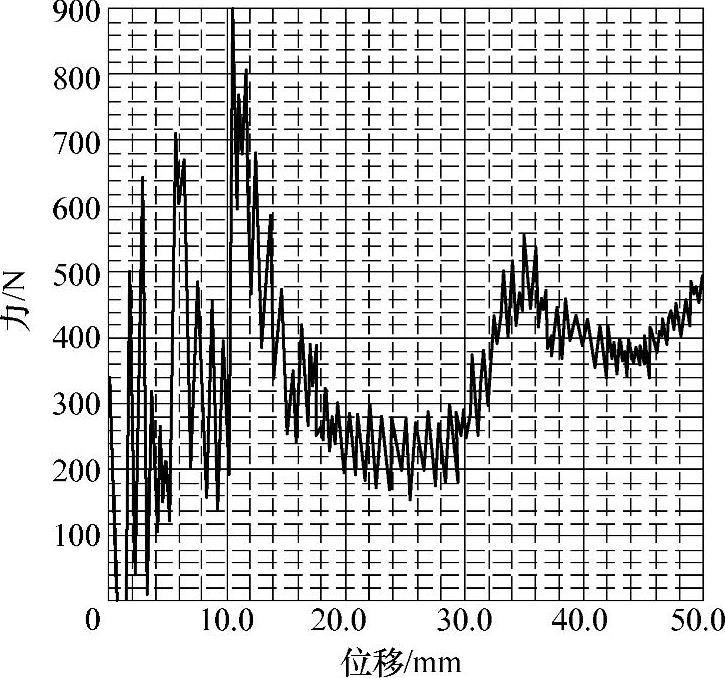(www.zuozong.com)

图3-40 载荷、瓶盖的位移曲线

图3-41 大变形典型示例

（2）执行 大变形分析类似于静力分析，因为不是一下子加上全部载荷，所以必须指定载荷的加载增量（仅时间步的载荷增量）。因为非线性分析必须一边逐次计算中间状态，一边移向下一步，所以是一点点逐个加上载荷的。分析的结果与应力分析一样是应力和位移，然而多数情况下载荷和位移的关系（P—δ关系）尤为重要。图3-42中显示了典型的屈曲现象和它的P—δ关系，应力和变形的评价与应力分析的情况相同。

（3）必须进行大变形分析的例子 像撑杆跳的杆子和弹簧取它们屈曲后的变形情况那样，也有形成肉眼可看见的大的变形现象，然而也有的变形量虽小，也必须进行大变形分析的。图3-43显示这方面的事例。

图3-43a中求受到横向载荷的梁和板的端部的移动量δ。

图3-43b为受到横向载荷的两端固定的梁和板或周围固定的板和圆板，求它们的轴向及面内方向的内力f和反力R。

图3-43c中，对于受横向载荷的梁或板，载荷引起的变形为δ，求δ超过梁高和板厚状态的应力和变形。

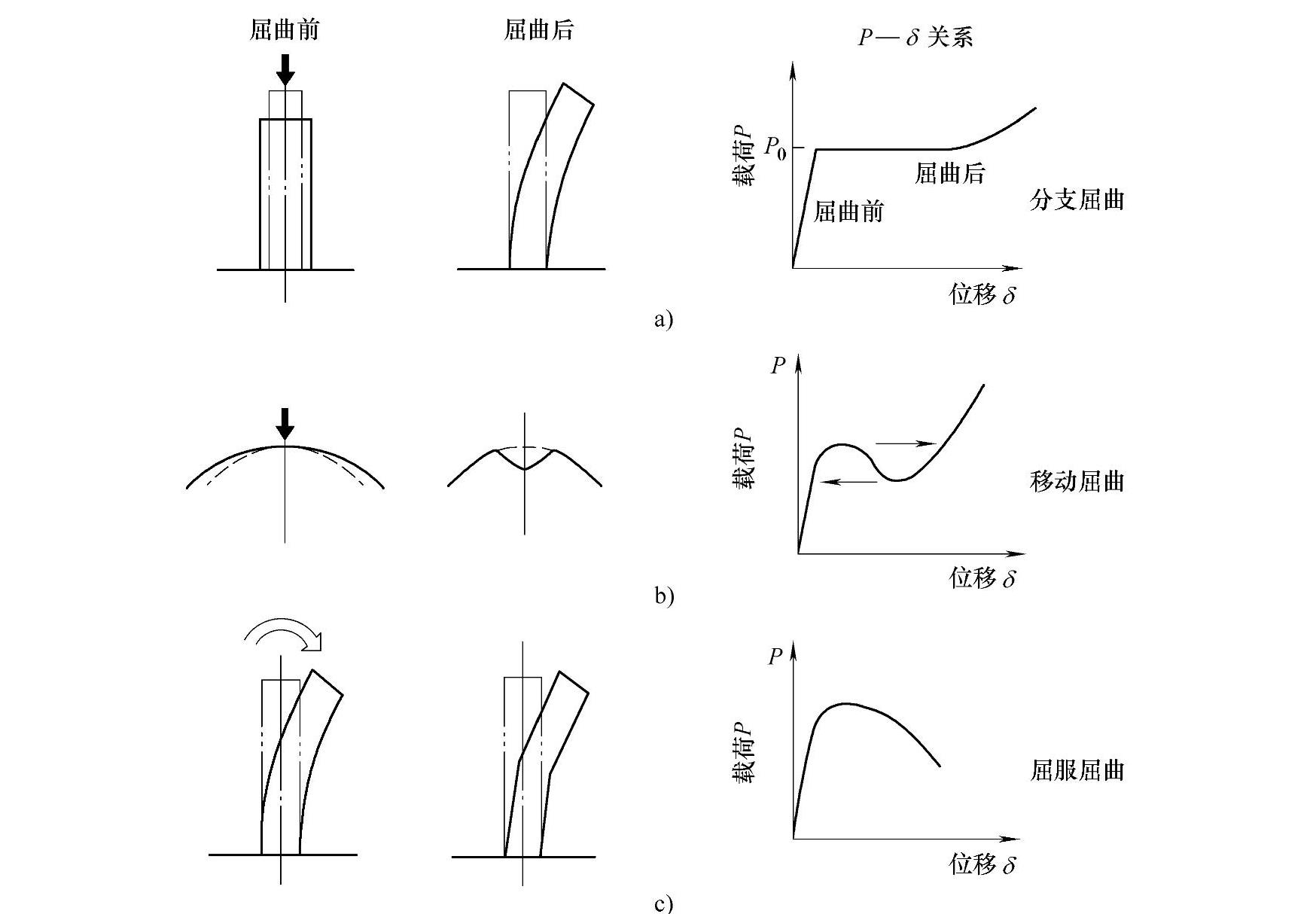
图3-42 典型的屈曲现象及其P—δ关系

a）柱 b）缶 c）管

图3-43d中求受到内压的椭园形管子的应力和变形。

图3-43b～d是变形量小，但伴随变形刚度变大的例子。加载初期载荷与弯曲应力相平衡，随着负荷的增加，除弯曲应力以外，面内膜应力也参与了平衡。在线性分析中，只能计算初始状态曲板引起的弯曲刚度，而进行大变形分析时，随着变形而产生的面内膜刚度的影响也要考虑到计算中去。

图3-44分析的是橡胶保护罩的大变形，这里可以用动画显示橡胶保护罩的变形，并与试验进行了对比。

5.热应力分析

热应力分析和应力分析相同，这种场合的载荷是温度，分析的结果是热应力和热变形。一般对物体来说，温度上升就膨胀（热膨胀），温度降低就收缩。伴随温度变化的热变形只要在全面的或局部约束住的情况下，就会产生热应力。它的大小是和约束了的变形量（应变量）成比例的。

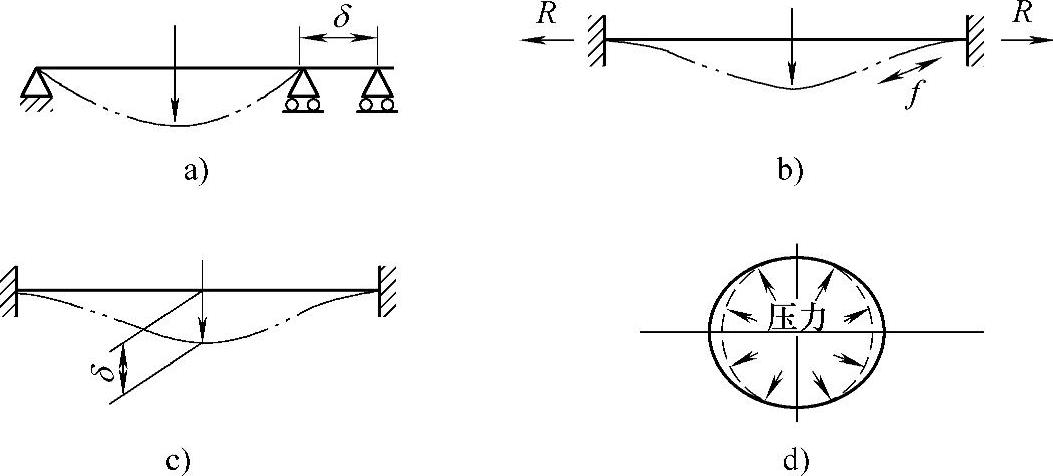
图3-43 大变形分析示例

例如铁轨的焊缝间隙夏天变小，这是由于铁轨受热膨胀变长了的缘故。到了秋天变凉，铁轨间隙就返回到原来的尺寸。也有由于异常的热，轨道的间隙无法再容纳轨道的伸长。这是无间隙状态，是轨道两头被约束了的状态。再发生热膨胀以至于不能伸长，轨道产生热应力，转道发生了弯曲现象。像这样发生膨胀如果没有阻止这种膨胀的约束起作用的话，也没有问题，多数是这种情况。然而如果有约束的话，由于存在没有预想的应力，就有变形和损坏的事情发生。

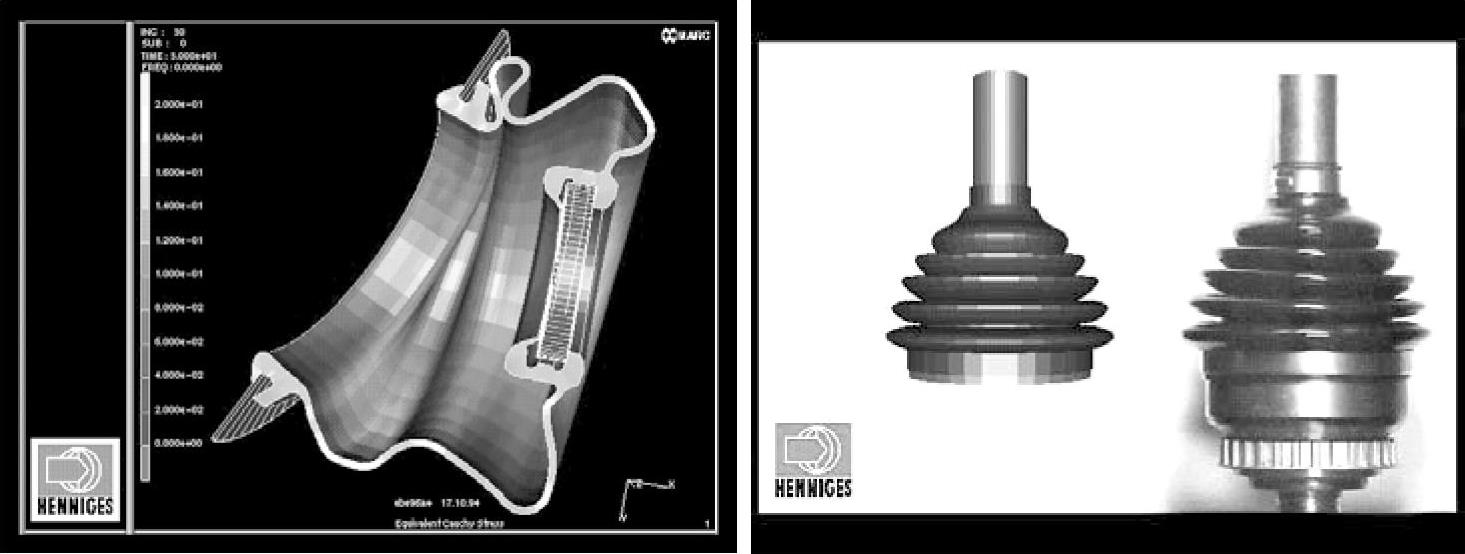
图3-44 橡胶保护罩的大变形分析和实验对比

另外，产生热应力的约束，就有如图3-45所示的那样，不仅仅由构件之间的约束而引起的约束，也有构件内温度的不均匀，由构件本身的内部约束引起的或者构件是由不同的线胀系数的材料构成的这种由构件本身的内部约束引起的。

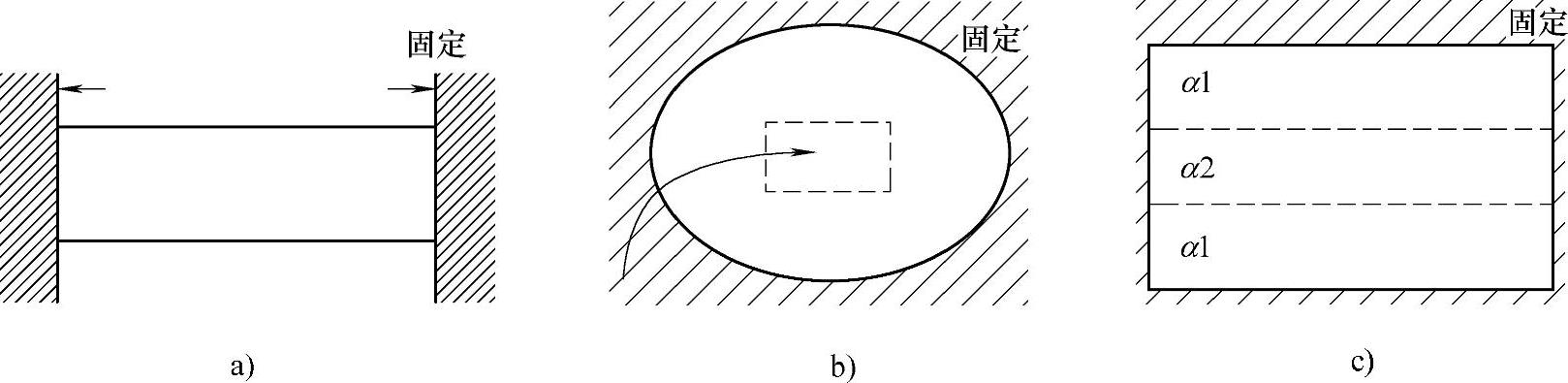
图3-45 热变形的约束和热应力

a）温度如果上升则为压缩应力，下降的话则为拉伸应力 b）比周围温度高则为压缩应力，低则为拉伸应力 c）线膨胀系数如果α2＞α1由于温度上升，则α2部分为压缩状态

如果构件随温度上升可以自由热变形，这个构件即使发生了热变形，但也不会产生热应力。反之，由于由周围而来的约束而不能产生热变形，即使不发生变形，但也会发生热应力。这与由机械的载荷产生的应力或变形不同，凭直觉容易出错。热变形分析的对象是校核有温度变化的某些机械的变形或间隙，还有双金属式温度计变形等。热应力分析的对象是热水管套、套管容器、传热板、内燃机、锅炉、蒸汽机、燃烧器和铁轨等。

分析的实行从程序启动到应力分析实行的顺序与基本应力分析相同。载荷成了温度变化量，要定义基础温度（参考温度）和分析时的温度，作为材料常数，线胀系数是必要的。其模型化可从如下几个方面入手：

1）单元对应于作为分析对象的结构使用梁单元、板单元、实体单元，这和应力分析相同。作为载荷要给出节点温度或单元温度。对于全部节点都要定义温度。

2）分析领域和边界条件约束条件的定义和通常应力分析没什么变化。必要时也要利用对称性。载荷成了热（温差）。为了求得分析对象的温度分布，首先进行热传导分析，利用它的结果再进行热应力分析。这种场合使用热传导分析用过的模型形状（单元、节点）不需要改动，就这样直接使用。但必须重新设定热应力分析所用的材料或单元特性。

3）单元划分细化应力集中的某个部分与通常的应力分析相同，其他请参考应力分析。

4）线膨胀系数热变形由α△T和约束程度决定，热应力由Eα△T和约束程度决定。热变形约束少则大，热应力约束多则大，都与线胀系数α成比例。这里，△T是温度差，E是纵弹性模量。用于热变形或热应力分析的线膨胀系数α，取从基础温度（热变形或热应力为0的状态）到使用温度（求热变形或热应力状态）的范围内的平均线胀系数（通常叫线胀系数）。

5）图3-46a中产生了相当于构件的初始温度（20℃）和最终温度（60℃）之差为40℃的应力。图3-46b中，因全体热膨胀不受约束，全体变形就大，应力仅仅是温度不均（55～60℃）而引起热膨胀约束的那部分应力。即使构件的最高温度同为60℃，图3-46b中20℃和60℃差40℃热应力会发生，图3-46b中55℃和60℃差5℃也会发生热应力。然而应力的大小相差1位。这差异应表明，一般来讲，热应力对约束条件敏感。如图3-46b所示，输入温度（部分有温差）分布不正确，应力就会产生很大的误差。

从实验求得少量温度数据，再用计算来分析热应力是相当困难。分析需要全部的节点温度，然而测量点部分以外的温度，用内插等来求出并输入的话，是不可靠的。由FEM进行热传导分析应该能如期顺利地求得全部节点的温度。

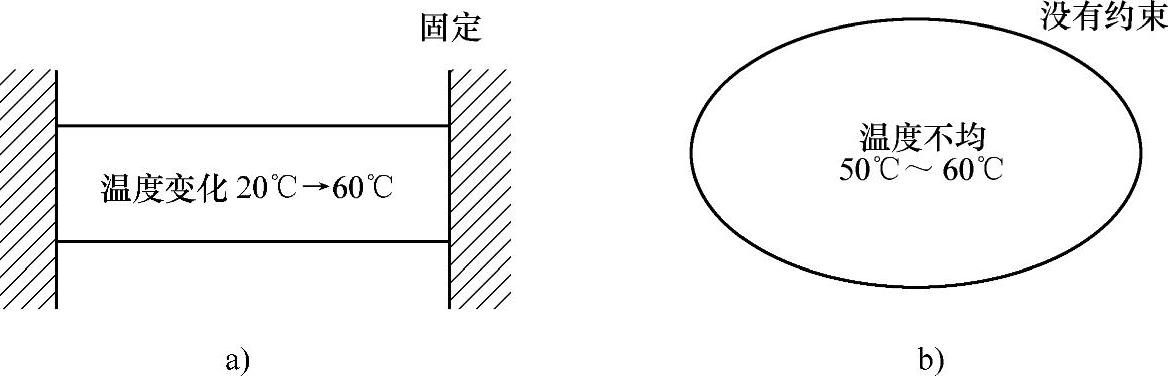
图3-46 热变形的影响

作为分析结果，求得热应力和热变形。热应力是从应变的平衡决定应力，如是韧性材料的话，允许应力超过屈服点。热变形有时要比预想的要大，必须注意间隙或接触问题。有温差或有温度变化的机械结构经常发生热变形和热应力，这些都可用有限元法求得，预先知道大致的标准就更方便。

铁为（100℃ 1m 1mm）（100℃温度变化，长度1m变化约1mm）。约束不允许伸缩1mm，就产生材料的屈服应力近似200MPa（20kgf/mm²）的热应力。热应力是由基本的Eα△T决定的，E为弹性模量，α为线膨胀系数，△T表示变化前后的温差。这里必须注意，热应力与剖面积等的构件尺寸没有关系。

当然，使热应力发生约束的一侧，因为大多是与该构件组合在一起的结构，并不是完全没关系，使应力降低的办法与通常的机械载荷场合不同。作为极端的例子，如图3-45a那样考虑在两端完全约束下的热膨胀的情况，温度的变化量如果相同的话，在构件内产生的热应力，即使它的剖面面积变成原来的两倍也完全相同。而由机械载荷引起的拉伸应力的话，如果剖面面积变成两倍的话，则应力就变成1/2，在热应力处理时不要忘记这差别。热应力对应于约束受到泊尔松比ν的很大影响。在单轴约束下的Eα△T为基础，两轴约束时以Eα△T/（1_-ν）计算，则约其1.4倍，三轴约束以Eα△T/（1-2ν）计算，则为其2.5倍。