基于对数似然比的优化湍流检测算法

从湍流区反射回的雷达信号是一个相关随机过程，两个连续脉冲之间的同一分辨体反射信号的相关系数r是多普勒速度的均方根σV值的函数［180］，即r＝f（σV）。

信号与噪声之间的特性用相关因子ρ来表示，即

式（4.58）中的γ表示信噪比SNR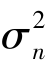，表示噪声方差，k是与气象雷达特性有关的空间因子。式（4.57）中的相关系数r采用

式中，Ts是脉冲重复周期，λ是气象雷达工作波长。综合式（4.57）—式（4.59）可得出相关因子ρ的表达式为

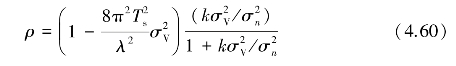
可看出相关因子ρ是非单调函数，在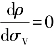时有最大值，由得

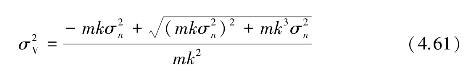
式中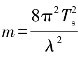，；结合式（4.58），在取得最大值时的信噪比为

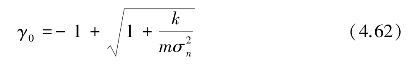
图4.17显示的是在不同的噪声功率σn下相关因子ρ和多普勒速度均方根值σV之间的关系（假设Ts＝0.001 s，λ＝0.03m，k＝1）；脉冲对方法是检测信号和噪声的相关因子ρ，当SNR大于等于式（4.62）的最大值时才适用。实际上，脉冲对方法是检测信号中相关因子的减少。在低SNR值下脉冲对方法的检测性能大大降低，这就导致湍流检测距离的减少。

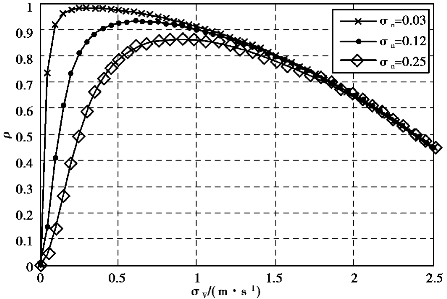
图4.17　相关因子ρ在不同噪声功率下与σV的关系

这里使用湍流多普勒速度均方根σV来对湍流等级进行分类，见表4.2。

表4.2　湍流等级分类

在湍流区域中，假设存在微粒S，则机载雷达的湍流观测示意图如图4.18所示。

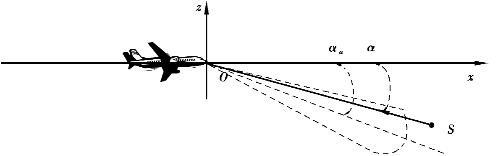
图4.18　湍流观测示意图

设飞机沿着x轴以恒定的速度V飞行，天线视角为αa，从散射体S返回的接收信号的多普勒频移为

λ为雷达发射波长，α是散射体S的方位角，天线波束宽度Δα的频谱展宽可由式（4.63）来估计［150］，即

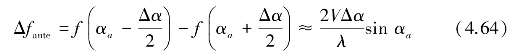
当V＝200m/s，λ＝3.2cm（载波频率为9 375MHz），Δα＝3°，αa＝90°，则由式（4.64）可得Δfante＝655Hz。

大气湍流的频谱展宽可估计为

σV是多普勒速度谱宽均方根，当Δfturb＞Δfante时，可判断为存在湍流目标，这就要求σV＞10m/s。根据表4.2，当σV≥5m/s时，就认为是相当危险的，则需要建立相应的湍流检测模型来提高其检测概率。

湍流检测是一个二元假设检测，其模型如下：

H0：不存在湍流目标；

H1：存在湍流目标。

用σv0表示其检测门限，则有

则输入检测系统的x（t）湍流信号检测模型如图4.19所示。

图4.19　湍流信号检测模型

图4.19中，s（t）为湍流信号，n（t）为高斯噪声。

用σ表示湍流幅度的均方根，设σ与多普勒速度谱宽的均方根σV具有线性回归关系，即

假设湍流信号回波是一个窄带过程，用相关函数描述为

式中，ω0为载频，此窄带过程的包络是个马尔科夫过程；则从状态i－1转移到i的条件概率密度函数为［116］(www.zuozong.com)

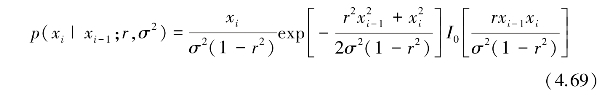
样本x1，…，xn的n维概率密度函数可由一维概率密度函数和条件概率密度函数来求出，即

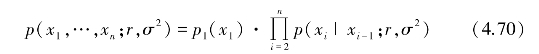
令一维概率密度函数p1（x1）服从瑞利分布，即

把式（4.69）和式（4.71）代入式（4.70）中，则得到样本x1，…，xn的多维概率密度函数。

其中，xi＞0，i＝1，2，…，n.

湍流检测可看成在不同参数假设下的问题。H0：σ＝σ0；r＝r0，H1：σ＝σ1；r＝r1，下标0和1分别对应湍流不存在和湍流存在的两种情形。

采用对数似然比准则，其检测准则主要是计算假设

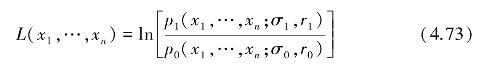
式中，p1（x1，…，xn；σ1，r1）是在H1假设下的多维概率密度函数，在H1下的σV取为4.5m/s，于是可根式（4.59）、式（4.67）求出相应的σ1，r1。p0（x1，…，xn；σ0，r0）是在H0假设下的多维概率密度函数，在H0假设下σV取为1m/s。同理，可求出相应的σ0，r0。

对于较大的x值，贝塞尔函数I0（x）具有近似值

把式（4.71）代入式（4.73），并结合式（4.74）；可得出检测算法

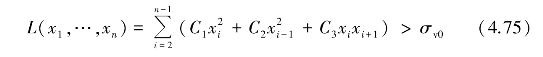
其中

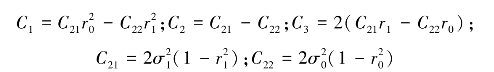
在H0假设下，设σV＝σ0＝1m/s；在H1假设下，设σV＝σ1＝4.5m/s；则可求出相应的C1，C2，C3。采用Monte Carlo方法对其进行仿真分析的步骤描述如下：

步骤1：初始化检测门限、处理次数M、样本量N，并令K＝0，m＝1。

步骤2：判断式（4.75）是否大于检测门限。若是，则执行K＝K＋1，并判断m是否等于M，若是则执行步骤4。

步骤3：若式（4.75）小于检测门限，则执行K＝K，并判断m是否等于M。若是，则继续执行步骤4，若否则重新返回判断。

步骤4：设进行M次处理，在每次处理中，令

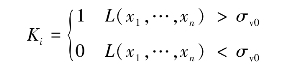
步骤5：计算检测概率，在M次处理中，超过门限的次数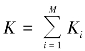，则检测概率为

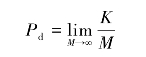
设气象雷达工作波长λ为0.03m，脉冲重复周期Ts为0.01s，运用Monte Carlo方法进行仿真分析。

图4.20和图4.21分别是在相同虚警率和信噪比、不同样本量下新的湍流检测算法与传统脉冲对算法的检测概率比较。

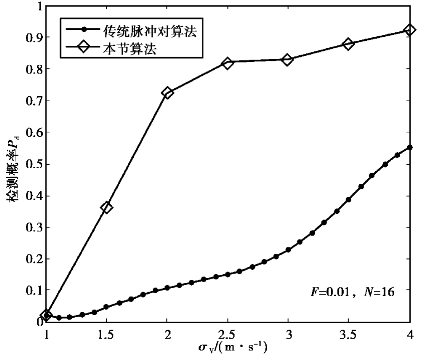
图4.20　N＝16下的检测性能

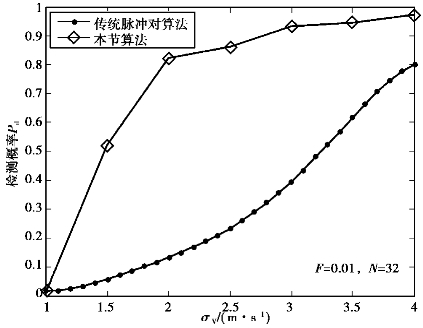
图4.21　N＝32下的检测性能

图4.20显示的是在虚警率F＝0.01、SNR＝10dB、样本量N＝16下的湍流检测性能。通过图4.20可以看出，随着湍流多普勒速度的均方根值的增大，其检测概率呈增大趋势；通过与脉冲对处理方法对比，其检测性能要优于传统的脉冲对检测方法45.26％。

图4.21显示的是在虚警率F＝0.01、SNR＝10dB、样本量N＝32下的湍流检测性能，通过与脉冲对处理方法对比，其检测性能要优于传统的脉冲对湍流检测方法47.51％。

图4.22和图4.23分别是在相同虚警率和样本量、不同信噪比下的新的湍流检测算法与传统脉冲对算法检测概率比较。

图4.22和图4.23考虑了非相干噪声的影响，图4.22和图4.23显示了在不同噪声水平下的湍流检测特性。图4.22和图4.23中，由于非相干噪声的存在，需要增加检测门限，这就导致检测算法效率的降低。

图4.22是在SNR＝10dB（F＝0.1，N＝16）下的检测概率特性图，其检测性能要优于传统的脉冲对检测算法48.92％；图4.23是在SNR＝20dB（F＝0.1，N＝16）下的检测概率特性图，其检测性能要优于传统的脉冲对检测算法55.34％。同时，通过比较在不同信噪比下的检测概率，发现SNR＝20dB下的检测性能要优于SNR＝10dB下的9.24％。

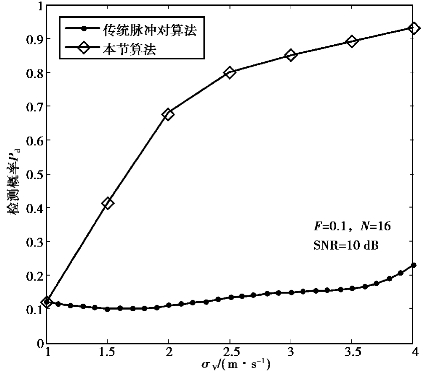
图4.22　SNR＝10dB下的检测性能

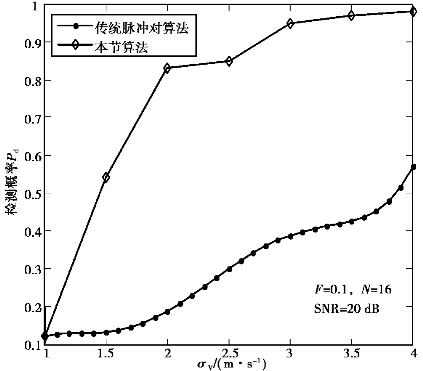
图4.23　SNR＝20dB下的检测性能

在低SNR下，本节提出的湍流检测算法的性能更加明显。这是因为传统的脉冲对湍流检测算法主要是检测相关因子的减少和非相干噪声，这就意味着为了得到相同的虚警率，其检测门限要相应地增加，这也说明了脉冲对算法为什么在SNR＝10dB或更小的情形下其检测效率会急剧减小。